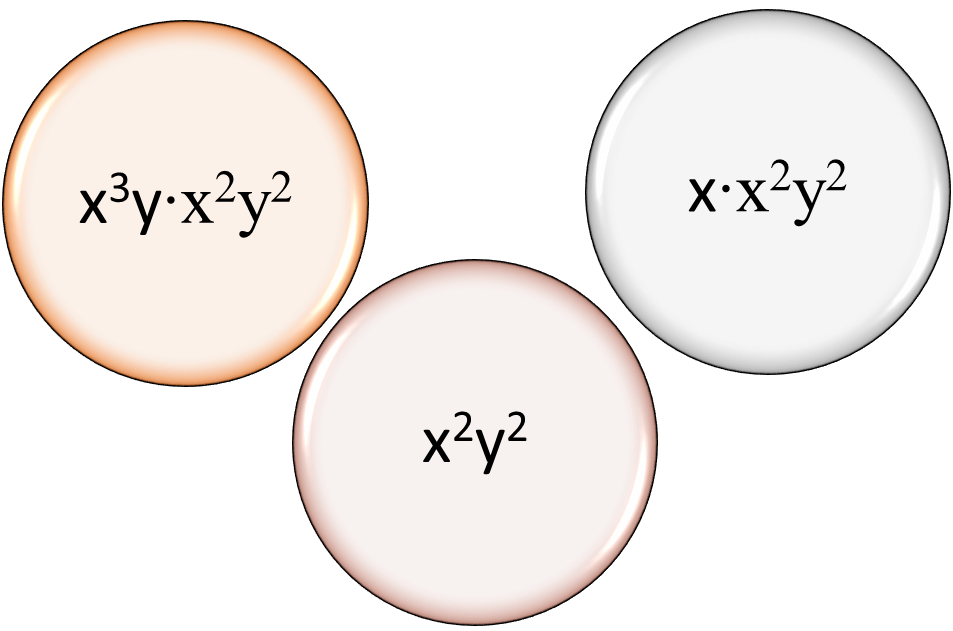Overview
Factoring a monomial from a polynomial is a process of finding the greatest common factor for the constants, the greatest common factor for the variable terms, and then using the distributive property to factor out the greatest common factor (GCF).
Identifying Factors
In symbol form, if a ∙ b = c, then both a and b are factors of c. Suppose the monomial is 10x4. There are the factors of 10 and the factors of x4. The factors of 10 are 1, 10, 5, and 2. The factors of x4 are x, x2, x3, and x4. They can be combined as 10 ∙ x4, 10x∙x3, 10x2∙ x2, and so on.
Greatest Common Factor of Constants
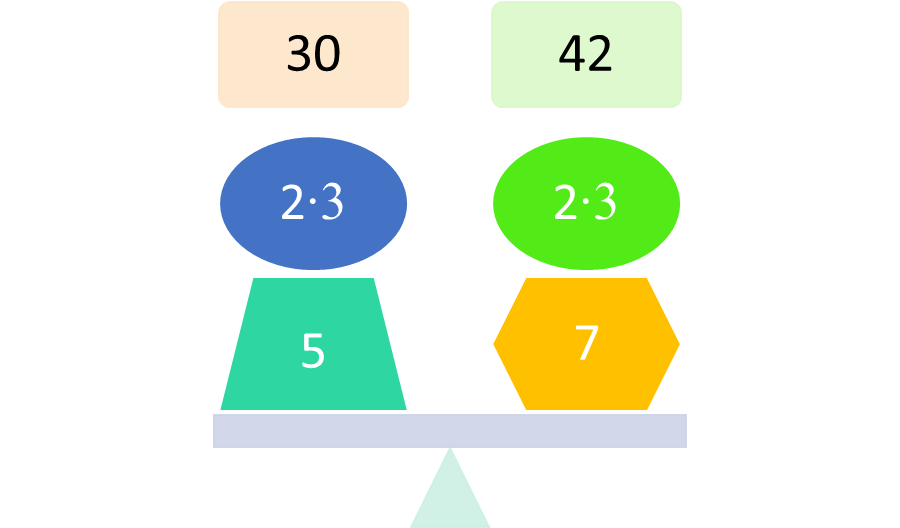
Finding the greatest common factor of two constants is a matter of finding the factors of both constants and checking to see what factors are in common. For example, the number 30 can be factored as 2∙3∙5 and the number 42 can be factored as 2∙3∙7. Their GCF, or greatest common factor is 2∙3, or 6.
Figure 1: Finding the GCF of constants.
Greatest Common Factor of Terms
Finding the GCF of two or more variable terms is also a matter of finding the factors of the variable terms, and seeing what factors are in common. Suppose the terms are x5y3, x2y2, and x3y2. The GCF will be the highest power of the common variables, or x2y2. If the terms were xy3, x4, and xy3, the GCF would be x. All three terms have x in common, because there is no y term in x4, but the highest power is x1 or x.
Figure 2: Finding the GCF of terms.
Factoring a Monomial from a Polynomial
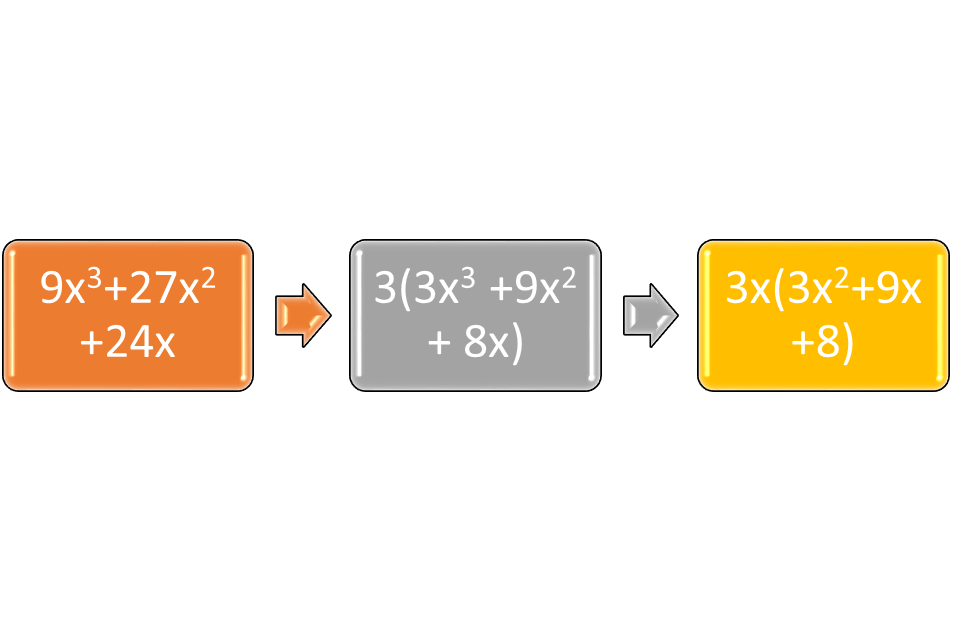
The first step in the process of factoring a monomial from a polynomial is to find the GCF of the constants and the terms. Suppose the polynomial is 3x2 + 6x + 9. The GCF of the constants is 3, because 3∙1 is 3, 3∙2 is 6, and 3∙3 is 9. There is no x term in common, because 9 does not have a variable associated with it. The second step in the process is to use the distributive property to factor out the GCF from each of the terms of the polynomial, so that the result is 3(x2 + 2x + 3). For example, if the polynomial is 9x3 + 27x2 + 24x, the constants factor as 3∙3, 3∙9, and 3∙8, so the GCF is 3. There is also a common variable in each term of the polynomial. Therefore, the GCF is 3x, and the result is 3x (3x2 + 9x + 8).
Figure 3: Factoring a monomial from a polynomial.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Erlanger, KY: visit Tutoring in Erlanger, KY