Overview
Trinomials are a special type of polynomials that have three terms, usually a squared term, a coefficient times the term that is to the first power, and a constant. In this review, the squared term has a numerical coefficient of 1.
Trinomials when the Squared Term Has a Coefficient of 1
The type of trinomial when the squared term has the coefficient of 1 has the form x2 + bx + c, where b, c, and x are real numbers. In the trinomial x2 + 7x + 12, x2 has the coefficient of 1, because 1x2 is the same thing as x2 using the multiplicative identity of 1. The number 7 is the coefficient of the second term x, and 12 is the constant. In the trinomial x2 – 5x + 6, the coefficient of the second term is -5 and the constant is 6. In the trinomial x2 + 2x – 24, the coefficient of the second term is 2 and the constant is -24.
Figure 1: The squared term has the coefficient of 1, the second term has the coefficient of 7 and the constant is 12.
Finding the Factors
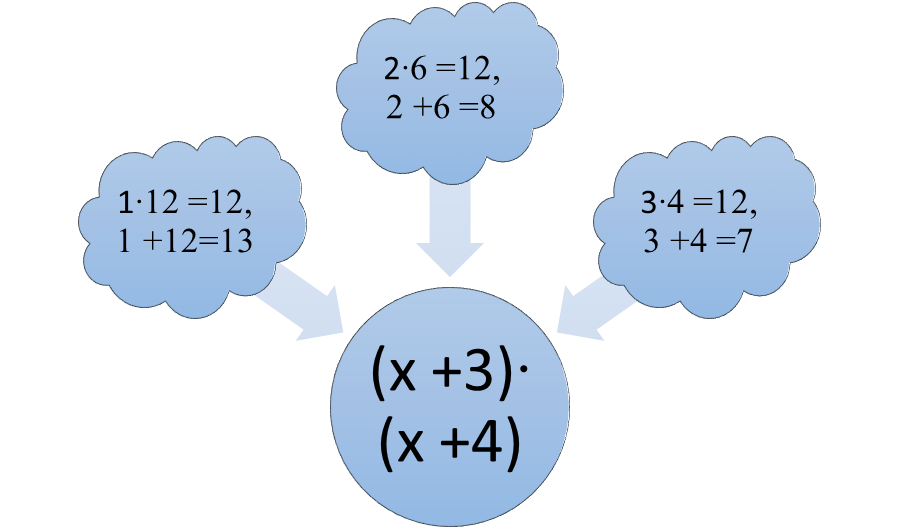
A trinomial is factored when the factors (x + y)(x + z) are determined. When the factors are multiplied using the FOIL method, the result is the original trinomial. If the trinomial can be factored, the constant will equal the product of the two terms yz. The coefficient of the second term will equal the sum of the outer terms and the inner terms. Suppose the trinomial is x2 + 7x + 12. The number 12 has several factors, 1 and 12, 2 and 6, 3 and 4. In order to choose between them, the sum of the pairs of factors must equal the coefficient of the second term, or 7. The factors 1 and 12 add up to 13, so they won’t work. The factors 2 and 6 add up to 8, so they won’t work. The factors 3 and 4 add up to 7, so the factored form of x2 + 7x + 12 must be (x +3)(x + 4). Using the FOIL method, (x + 3)(x + 4) is x2 + 4x + 3x + 12 or x2 + 7x + 12.
Factoring when the Constant Is Positive
If the constant is positive, the factors of the constant must have the same sign, either positive or negative. The way to determine the sign of the factors of the constant is to look at the sign of the second term. Suppose the trinomial is x2 + 7x + 12. Both factors must be positive, and both 3 and 4 are positive numbers that add up to 7. Suppose the trinomial is x2 – 5x + 6. In this case, the sign of the second term is negative (-5), so both factors must be negative. The negative factors of 6 are -1 and -6, and -2 and -3. In this case, -2x and -3x add up to -5x, so the factored form is (x – 2)(x – 3). Using the FOIL method, (x – 2)(x – 3) is x2 -2x – 3x + 6 or x2 – 5x + 6.
Figure 3: Multiplication of positive and negative numbers.
Factoring when the Constant Is Negative
If the constant is negative, the factors of the constant must have different signs. Suppose the polynomial is x2 + 2x – 24. Some of the factors of -24 are 1 and -24, 2 and -12, and 6 and -4. In this case, 1 and -24 add up to -23, 2 and -12 add up to -10, and 6 and -4 add up to 2. The factored form is (x + 6)(x – 4). Using the FOIL method, (x + 6)(x – 4) is x2 + 6x – 4x – 24.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Presque Isle, ME: visit Tutoring in Presque Isle, ME