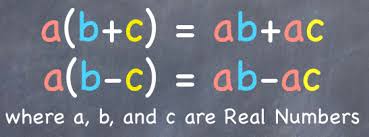Overview:
The Distributive Property in math can be used to solve equations by combining like terms. It is another tool to simplify complicated problems by using common patterns of multiplication over addition or subtraction.
Definitions:
|
Figure 1: Formal definition of the Distributive Property |
In arithmetic, the distributive property was defined with examples such as 4(3 + 4) = (4∙3) + (4∙4), which simplifies to 28 =12 + 16. Similarly, 5(10 – 3) is the same thing as (5∙10) – (5∙3) which simplifies to 35 = 50 – 15. Using variables, the distributive property holds true.
Combining Like Terms:
Expressions can be combined that use the same variables because of the Distributive Property. For example, 9x + 2x = 11x because it follows the same pattern, as (9 + 2)x =11x. Similarly, 8x – 4x = 4x because it follows the pattern (8-4)x = 4x. Even a more complicated expression such as 9ab2-6a2b can be factored as 3ab(3b – 2a) because 3ab(3b) – 3ab(2a) = 9ab2 – 6a2b. Suppose that the expression were made even difficult looking, as (9ab2 – 6a2b)/(3b – 2a). That expression could be simplified to 3ab, by using the Distributive Property.
Geometric Explanation of the Distributive Property:
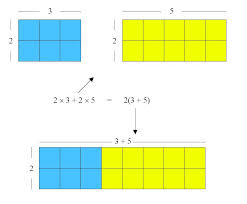
Suppose that one rectangle has width c and length a + b. The area of the rectangle, c(a +b), is the same whether it is calculated as the measurement of one rectangle, or the sum of 2 rectangles, ca + cb. This property can be used to solve equations where parentheses are used. For example, suppose the expression is 8(y + 1). The parentheses can be eliminated by multiplying, or 8y + 8, and then the rest of the equation can be solved.
|
Figure 2: The area of the rectangle is the same whether it is calculated as c(a +b) or ca + cb |
Applications of the Distributive Property:
Word problems involving discounts, tips, taxes, and overtime can all be solved using applications of the Distributive Property. Suppose the question were, “If the sale price of an item is $15.00, and it is being offered at a 20% discount, what is the regular price?” If the regular price is x, then the sale price is (1-.20)x or .80x. Solving for x, the regular price is $18.75. It can be checked by subtraction using the Distributive Property, as the sale price will be equal to the regular price of $18.75 – the 20% discount of $3.75, or $15.00. That also follows the pattern of c(a – b) =ca – cb. Suppose a person is paying 9% sales tax on a purchase. This would be the same as paying for the item and 9% of the item, or paying the price of the item +.09 of the price. If the price of the item is $18.75, the price plus tax is 1.09(18.75) or 20.4375 which the store will round up to $20.44. In order to check the figures, the Distributive Property could again be used, so that $20.4375 = $18.75 +1.6875.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Lexington, NE: visit Tutoring in Lexington, NE