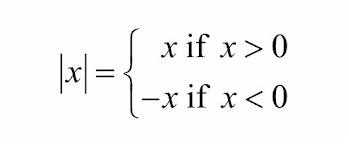Overview
Absolute value functions are functions in which f(x) = │x│. They are important in a number of settings, including the study of error and probability functions.
Definition of Absolute Value
Absolute value is a measure of the distance of a number from 0. For any real number x, both x and –x have the same absolute value, equal to the positive value of x. For example, both 3 and -3 have the same absolute value, 3, because both numbers are the same distance from 0 on the number line. The number 3 is 3 units to the right of 0 on the number line, and the number -3 is 3 units to the left of 0 on the number line.
Figure 1: Definition of absolute value in symbol form.
The Absolute Value Function
The absolute value function can be graphed with ordered pairs for each value of │x│, such as (3, 3), (2, 2), (1, 1), (0, 0), (-1, 1), (-2, 2), (-3, 3) and so on. The line forms a perpendicular angle with vertex at (0, 0) that is symmetrical on both sides of the y axis.
Figure 2: Graph of the absolute value function.
Study of Error
The study of error and some other complex situations follows an absolute value function. Suppose that an experiment is conducted, so that time is estimated to the nearest second. Students are asked to estimate the amount of time a minute will take. The amount of error can be measured as the distance from 60 seconds, so that an estimate of 63 seconds and an estimate of 57 seconds has the same value, │3│. Any function that depends on distance from a target will show a similar distribution.
Probability Functions
One type of probability function is the probability of getting a value from 1-12 when rolling a pair of fair dice. There are 36 possible combinations. Rolling a 2 [(1, 1)] has a probability of 1/36, rolling a 3 [(1, 2), (2, 1)] has a probability of 2/36, rolling a 4 [(2, 2), (1, 3), (3, 1) has a probability of 3/36, rolling a 5 has a probability of 4/36, rolling a 6 has a probability of 5/36, and rolling a 7 has a probability of 6/36. However, rolling an 8 has the same probability, 5/36, of rolling a 6, rolling a 9 has a probability of 4/36, rolling a 10 has a probability of 3/36, rolling an 11 has a probability of 2/36, and rolling a 12 has a probability of 1/36. It also follows an absolute value function.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Logan, UT: visit Tutoring in Logan, UT