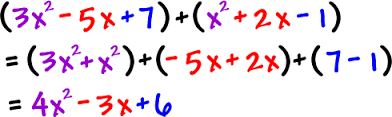Overview
Adding and subtracting polynomials is similar to adding and subtracting other expressions. Terms can be combined using the Commutative and Associative properties for addition, then like terms can be added or subtracted as needed.
Find Like Terms
Recall that like terms have the same variables and are at the same degree. If they have the same degree, the terms are raised to the same power. For example, 4x and 2x can be added or subtracted because they both have the variable x and no other. Addition of 4x + 2x equals one term, the monomial 6x. They are also at the same degree, because both 4x and 2x have the same exponent 1. The expressions 3x2 and 4x both have the variable x, but they are not at the same degree, as 3x2 has degree 2, and 4x has degree 1. Combining them will result in the polynomial expression 3x2 +4x.
Use Properties
Polynomials can be rearranged using the Commutative Property without changing their value. For example, 4x + 2x has the same meaning as 2x +4x. This was already shown in rearranging polynomials in standard form, so that 5x + 6x3 +109 +8x2 can be rearranged to 6x3 +8x2 + 5x + 109. The Associative Property also applies, so that (6x3 +8x2) + (5x + 109) equals 6x3 + (8x2 + 5x + 109). The one thing to remember when using either property with polynomials is that the sign in front of each term must stay with that therm. Therefore, 8x2 + 5x -109 + 6x3 can be rearranged as 6x3 +8x2 +5x -109.
Adding Polynomials
In order to add polynomials, first find like terms, rearrange them using the Commutative Property, and combine like terms using the Associative Property. For example, (2x2-x) +(x2 +3x -1) have the like terms of 2x2 +x2, -x +3x, and the constant -1. Notice that the negative signs stay with the terms –x and -1. The new expression, using all the terms, is 2x2 +x2 –x +3x -1. Combining terms, (2x2 +x2) +(-x + 3x) -1 results in a new expression where (2x2 +x2) can be replaced by 3x2, and (-x +3x ) can be replaced by 2x , so the simplified expression is 3x2 +2x -1.
Subtracting Polynomials
Subtracting is the inverse of addition, so the difference between adding and subtracting polynomials is that each term subtracted has the opposite sign. For example, -(2x3 + 4x2 +12x +42) is -2x3-4x2-12x -42 and –(2x2-12x – 36) is -2x2 +12x +36. Therefore, (a4-2a) –(3a4 -3a -1) is the same thing as adding a4 -2a -3a4 +3a +1. Like terms can be arranged, so that a4-3a4 -2a +3a +1is the same expression. Then like terms can be combined, as -2a4 +a +1.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Mount Pearl, NL: visit: Tutoring in Mount Pearl, NL