Overview
Numbers in Base 2 are real numbers that can be involved in mathematical operations in the same way as more familiar decimal or Base 10 numbers. The advantage of binary systems — that they contain two numerals 0 and 1 — means that they can be used in situations that have two alternatives.
Introduction to Base 2
Base 2, or binary, is the smallest grouping possible. In Base 2, 0 means 0, 1 means 1, and 102 means 2, 112 means 3, 1002 means 4, 1012 means 5, 1102 means 6, 1112 means 7, 10002 means 8, 10012 means 9, and 10102 means 10 in the decimal (Base 10) system. Notice that place value follows the same pattern in both bases. 100 is 1, and 20 is 1, 101 is 10 and 21 is 2, 102 is 100 and 22 is 4, represented in Base 2 as 1002; 103 is 1000, and 23 is 8, represented in Base 2 as 10002. The difference is that a number such as 102 (which means 2) is read either as “two” or “one-zero”, 1002 is read as “eight” or “one-zero- zero”, and so on.
Addition and Subtraction of Binary Numbers
Binary numbers add, subtract, multiply, and divide according to the same rules as numbers in any other base. Addition of two binary numbers involves carrying, similar to adding numbers in Base 10. Suppose the numbers to be added are 1100112 and 100012. Adding from right to left, the sum is 10001002, because adding 1 and 1 in Base 2 equals 102. Subtraction uses similar additive inverse rules to other systems, so that subtraction means adding a negative number. More borrowing is used than in Base 10 subtraction.
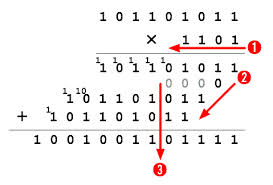
Multiplication and Division of Binary Numbers
Multiplication in Base 2 follows a similar repeated addition model as multiplication in decimal systems, and division in Base 2 follows a similar repeated subtraction model as division in decimal systems. Suppose that 1102 is multiplied by 1012. Partial products are used, so that the first row [1102 times 12] is 1102, the second row is [1102 times 0] moved to the left one space, and the third row is [1102 times 12] moved to the left 2 spaces. The entire product is 111102. It really helps to use graph paper or columnar ruled paper to keep the columns in line while adding or subtracting them.
Fractions in Base 2
Converting fractions or decimals into the binary Base 2 system presents a challenge, because many fractions and decimals that are exact in the decimal system have approximate values. The decimal 0.10 has an approximation in Base 2, and so do fractions such as ¼, 1/3, ½, and many others. Operations in Base 2 with fractions are approximate, called “floating point arithmetic.”
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Paradise Valley, AZ: visit: Tutoring in Paradise Valley, AZ