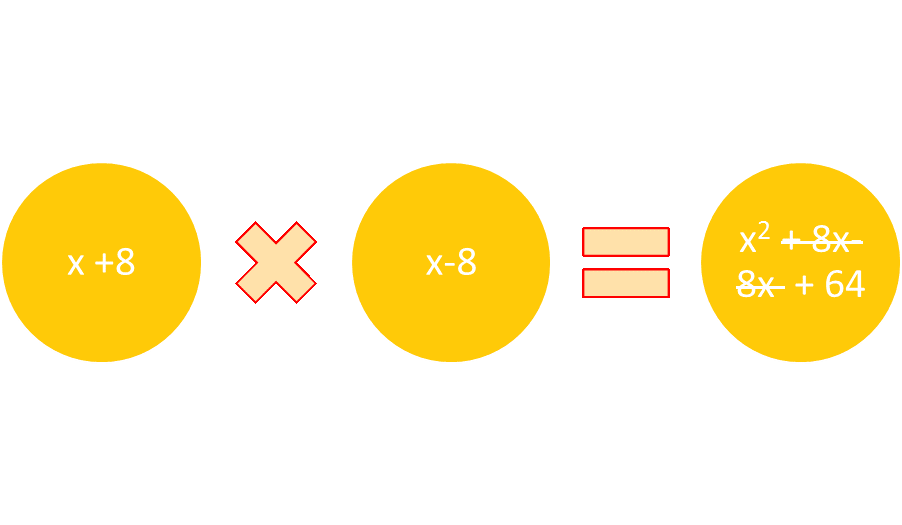Math Review of Difference of Squares

Overview

The difference of squares is a common binomial pattern that can be factored as (x+b)(x-b). It can be used in situations involving estimation by making both elements a difference of squares.

Perfect Squares

In order for the pattern to work, both elements must be perfect squares. The variable x² is a perfect square. So is 9x⁴, as it can be factored as (3x²)². Similarly, the numbers 36(6²) and 81(9²) are perfect squares. The monomial 100x² can be factored as 10x(10x).

Difference of Squares

Suppose the expression were 25x² – 144. Both 25x² and 144 are perfect squares. The monomial 25x² can be factored as 5x∙5x and 144 can be factored as 12∙12. The entire expression can be factored as (5x +12)(5x -12). The middle terms 5x∙12 and 5x∙-12 cancel each other out.

Figure 1: The pattern for the difference of squares shows that the middle terms cancel each other.

Using Estimation

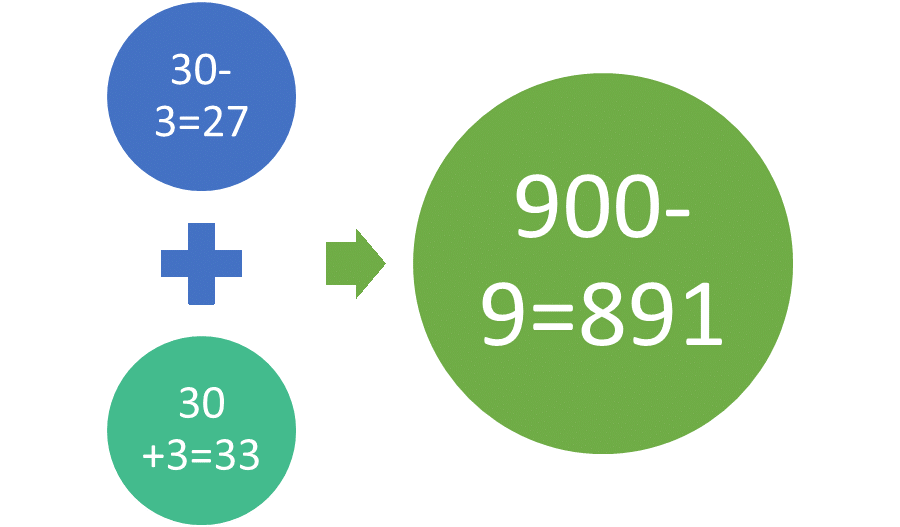
A math problem such as 27∙33 can be estimated as the difference of squares. The mean of 27 and 33 is 30, so 27 times 33 can be expressed as (30 – 3)(30 + 3) or 30² – 3² or 900 – 9 which is 891. In order to check, 27∙33 is 891.  Similarly, 56∙44 can be expressed as (50 + 6)(50 – 6) or 2500 – 36 = 2464, and 56∙44 is 2464.

Figure 2: An example of estimation using the difference of squares.

Geometric Representation

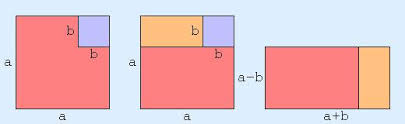
Suppose one square has the area a² and one corner with the area measuring b² is taken out of it. The resulting figure, a²-b², can be divided into 2 rectangles. One rectangle has the measurement of a(a-b). The other rectangle has the measurement of b(a-b). Adding the two rectangles together gives the measurement of (a+b)(a-b) for the same figure. The area of the figure is (a +b)(a-b), so a²-b² = (a+b)(a-b).

Figure 3: Geometric representation of the difference of squares.

Interested in geometry tutoring services? Learn more about how we are assisting thousands of students each academic year.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Edmonton, AB, Canada: visit Tutoring in Edmonton, AB, Canada