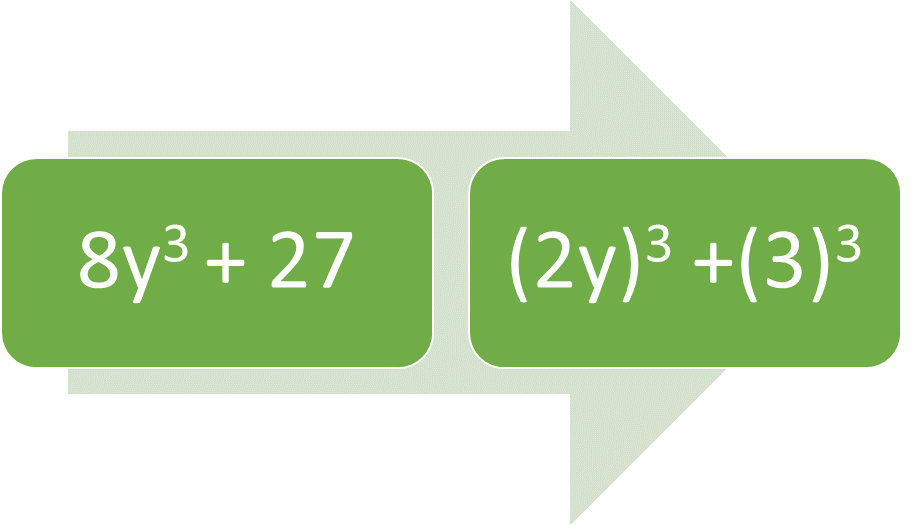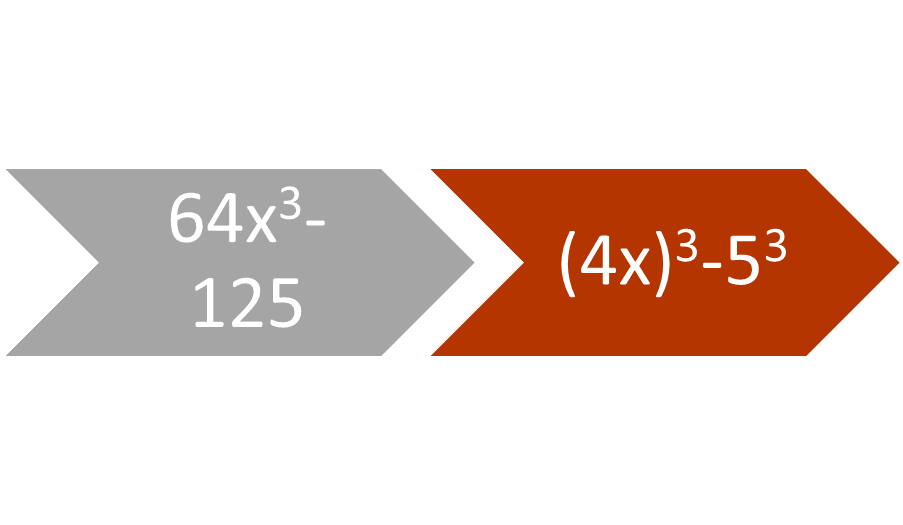Overview
Sums or differences of cubes can be factored similarly to other quadratic equations. They follow a pattern that is a little more complex than factoring quadratic equations.
Sum of Cubes
A sum of cubes is an expression such as x3 + a3, where both members of the expression are perfect cubes. Suppose the expression is 8y3 + 27. The monomial 8y3 is a perfect cube of 2y, because (2y)3 equals 8y3. Similarly, the constant 27 is a perfect cube of 3, because 33 equals 27.
Figure 1: The sum of cubes follows the pattern x3 + a3.
Difference of Cubes
A difference of cubes is an expressions such as x3 – a3, where both members of the expression are perfect cubes. Suppose the expression is 64x3 – 125. The monomial 64x3 is a perfect cube of 4x, because (4x)3 equals 64x3. Similarly, the constant 125 is a perfect cube of 5, because 53 is 125. A perfect cube can be a negative real number, because a negative real number times a negative real number is positive, and a positive number times a negative number is a negative number.
Figure 2: The difference of cubes follows the pattern x3 – a3.
Factoring the Sum of Cubes
The sum of cubes x3 + a3 follows a special pattern. One factor is (x + a), and the other factor is a quadratic polynomial that is already in simplest terms, (x2 – ax + a2). Multiplying (x + a) (x2 – ax + a2) is the same thing as adding x(x2 – ax + a2) + a(x2 – ax + a2). The first term is x3 – ax2 + a2x, and the second term is ax2 – a2x +a3. Putting the terms together, the entire expression is x3 – ax2 + a2x –a2x + a3. Simplified, the expression is the sum of cubes x3 + a3. Suppose the expression is 8y3 +27. Following the pattern, it can be factored as (2y + 3) (4y2 – 6y + 9).
Factoring the Difference of Cubes
The difference of cubes x3 – a3 also follows a special pattern. One factor is (x – a), and the other factor is a similar quadratic polynomial to the sum of cubes, also already in simplest terms, (x2 +ax +a2). Multiplying (x – a)(x2 + ax + a2) is the same thing as adding x(x2 + ax + a2) – a(x2 + ax + a2). Simplified, the expression is the difference of cubes x3 – a3. Suppose the expression is x3 – 216. Following the pattern, it can be factored as (x – 6)(x2 + 6x + 36). That is the same thing as x(x2 + 6x + 36) – 6(x2 +6x + 36). Putting the terms together, the entire expression is x3 + 6x2 + 36x – 6x2 – 36x – 216.
Figure 3: The pattern for factoring the sum of two cubes or the difference of two cubes.
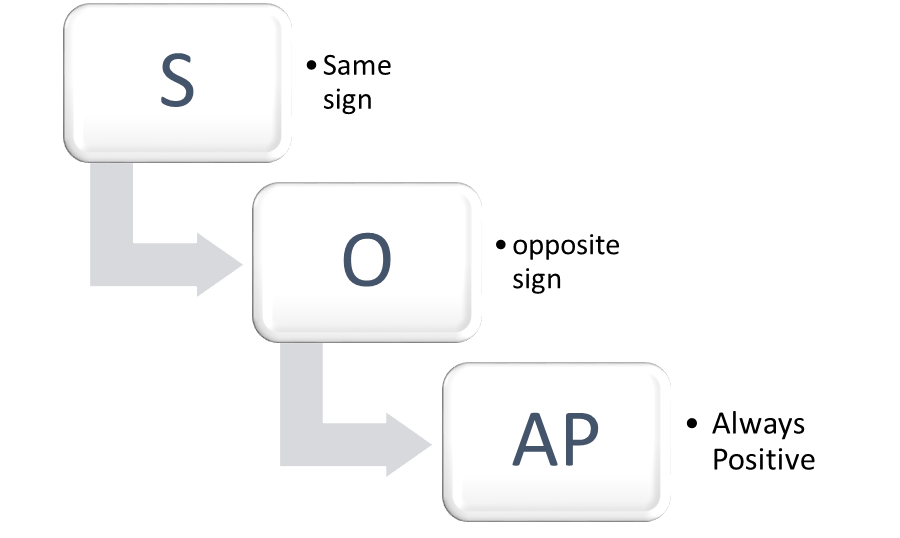
SOAP
The acronym SOAP is an easy way to remember the sequence for either the sum or difference of cubes. If the expression to be factored is a sum of cubes x3 +a3, the first factor (x + a) has the same sign as x3 + a3. The first operation (x2 – ax) in the second factor (x2 – ax + b2) has the opposite sign as x + a. The second operation in the second factor (ax + b2) is always positive. If the expression to be factored is a difference of cubes x3 – a3, the sequence also follows SOAP. The first factor is (x – a), the same sign. The first operation (x2 + ax) in the second factor (x2 +ax + b2) has the opposite sign as (x – a) and the second operation (ax + b2) is always positive. The proof of factoring either the sum of cubes or the difference of cubes will be explored in more advanced college mathematics classes.
Figure 4: A mnemonic to remember the order of signs. (It even floats!)
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Alabaster, AL: visit Tutoring in Alabaster, AL