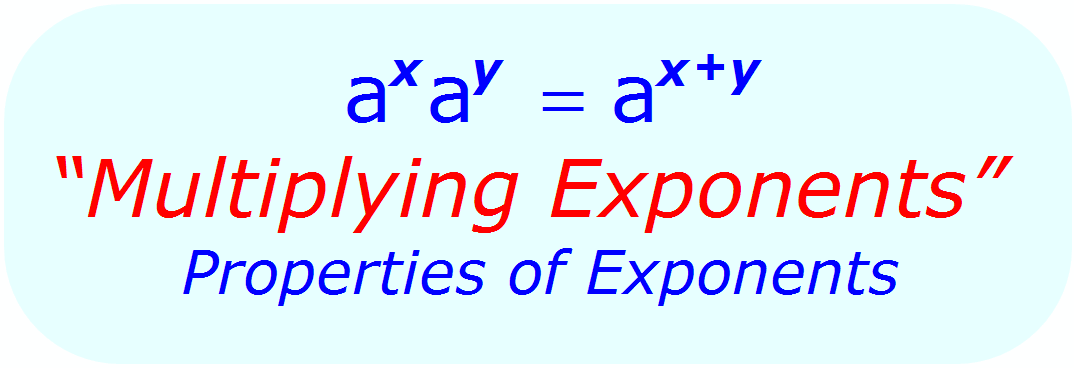Overview
Exponents are used as a type of shorthand directing how many times that a base number is multiplied by itself. Exponential expressions are useful when working with very large or very small numbers, as in scientific notation. Like other numbers and variables, exponential expressions can be multiplied following certain rules.
Review of Simplifying Expressions
If there are negative exponents in an expression, it is not simplified. The expression x-3 can be defined as 1/x3. Similarly, if the same base is used more than once in an expression, it is not simplified. Suppose the expression is x2x. That actually means x·x·x, or x3. Also, powers that are raised to powers are not simplified, such as [x5]2. If any coefficients have common factors, those common factors must be simplified. For example, (15a2)/ (10b3) can be simplified to (3a2)/ (2b3) because 15 and 10 have a common factor of 5.
Products of Powers
Since an exponent stands for how many times a base is multiplied by itself, the rule for multiplying exponents can be discovered by showing each power as repeated multiplication. If the expression is y3y2, that can be expanded as y·y·y·y·y, or y5. The product of the powers can be found by adding the exponents, as 3 +2 = 5. However, the bases must be the same in order for the exponents to be added. In the language of algebra, for any real number a not equal to zero, am·an = am+n.
Powers of Powers
Expressions such as [x5]2 actually mean x5·x5, or (x·x·x·x·x) (x·x·x·x·x), by using the meaning of exponents as repeated multiplication. The product of powers of powers can be found by multiplying the exponents, as 5·2 equals 10. In the language of algebra, for any real number a not equal to zero, (am)n=amn. The way to know whether to add or multiply the exponents is to expand the expression to repeated multiplication. For example, z3z4 means z·z·z·z·z·z·z, or z7, while (z3)4 means (z3)(z3)(z3)(z3), or (z·z·z)(z·z·z)(z·z·z)(z·z·z) or z12.
Powers of Products
An expression such as q5 only involves one component, the variable q. However, an expression such as (3z)3 has two components, the coefficient 3 and the variable z. It can be expanded as (3z)(3z)(3z), or 3·3·3·z·z·z, or 33z3, or 27z3. In the language of algebra, (ab)n, for any real number a and b not equal to zero and n as an integer, (ab)n equals anbn.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Burnaby, BC: visit: Tutoring in Burnaby, BC