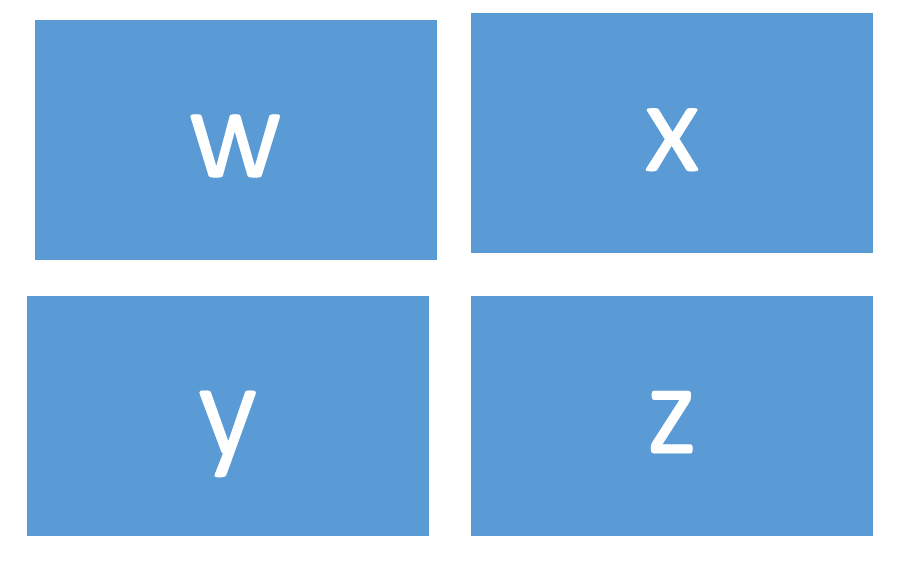Overview:
The dimensions of a matrix are important to its definition. In order for the multiplication of two matrices to be meaningful, each matrix must have certain dimensions. Multiplication of matrices is not commutative.
Review of Scalar Multiplication
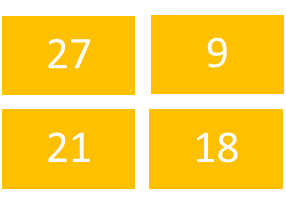
In order to multiply a matrix by a constant, every member of the matrix is multiplied by the constant. Suppose that matrix A consists of the members [wxyz]. Multiplying each member by a constant e means that the new matrix will consist of [ew ex ey ez]. Suppose Matrix B consists of [9 3 7 6]. Multiplying each member by 3 would lead to the new matrix [27 9 21 18].
Figure 1: Matrix A
Figure 2: In Matrix 1A, every element of Matrix A is multiplied by the constant e.
Figure 3: Matrix B is a 2 X 2 Matrix, in the same form as Matrix A, but the variables are replaced with real numbers.
Figure 4: In Matrix 1B, every element of Matrix B is multiplied by 3
What Dimensions Must the Matrix Be?
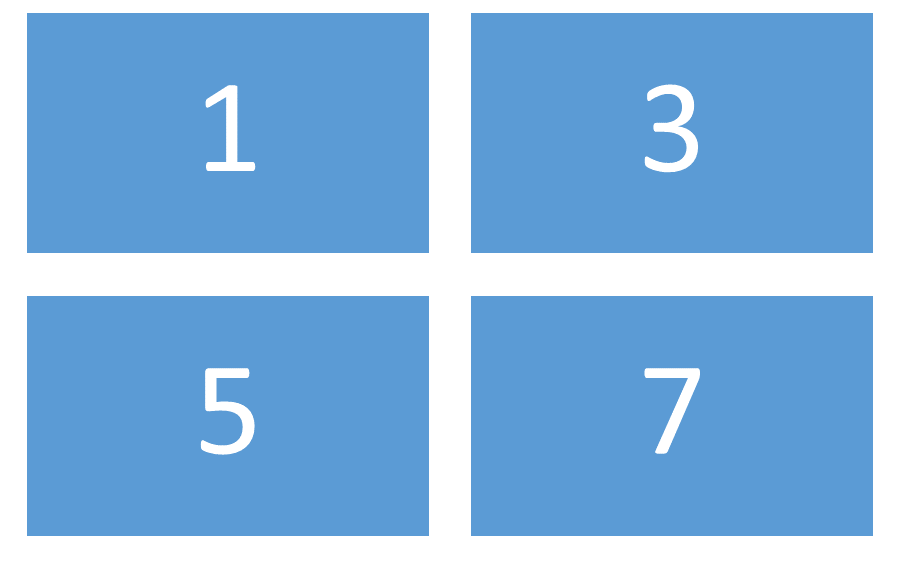
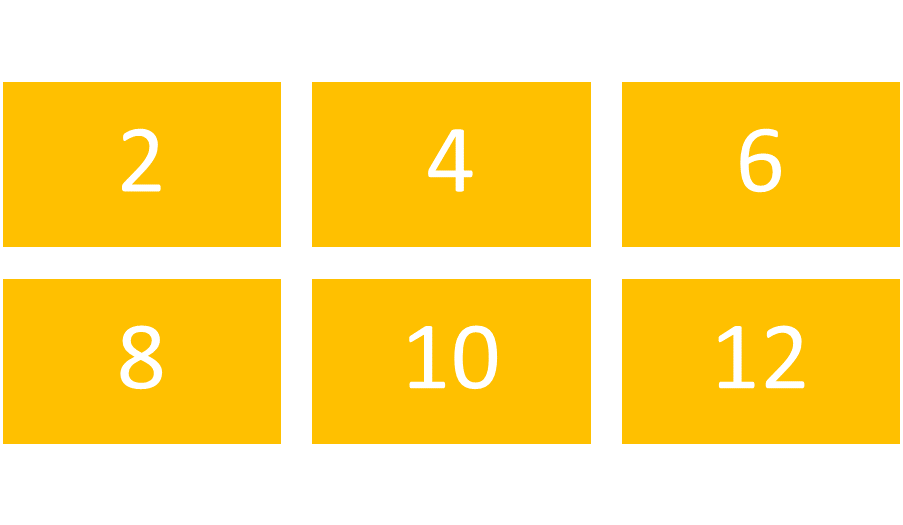
The first step in multiplying matrices is to determine the dimensions of each matrix. If the number of columns of the first matrix is equal to the number of rows in the second matrix, multiplying the matrices is possible. Suppose Matrix D consists of the elements [1 3 5 7] and Matrix E consists of the elements [ 2 4 6 8 10 12]. Matrix D has the dimensions 2 X 2 and Matrix E has the dimensions 2 X 3. Matrix DE would also have the dimensions 2 X 3. It would be equal to multiplying the elements of Matrix D by the elements of Matrix E.
Figure 5: Matrix D
Figure 6: Matrix E
What Is the Next Step in Multiplying Matrices?
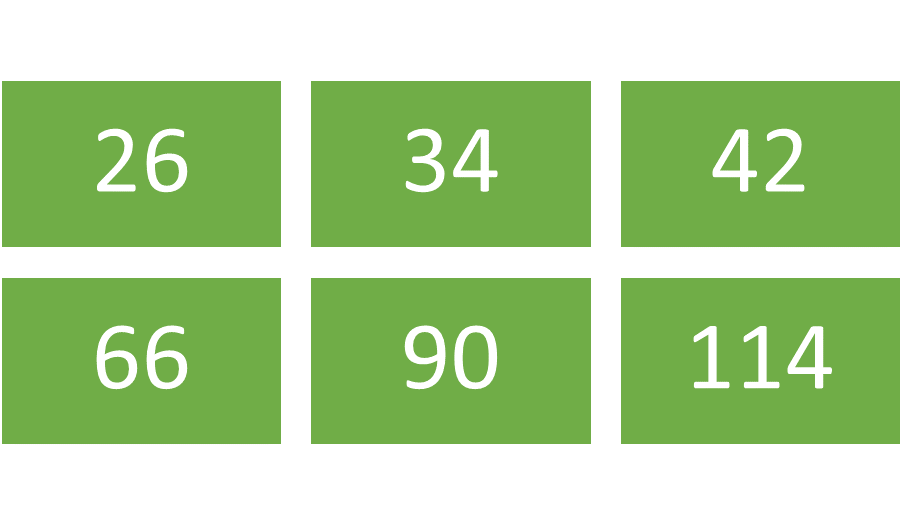
In the next step, multiply each element of the row in the first matrix by each element of the column of the second matrix, and add those products together to form the new elements of the product matrix. Using the example of Matrix DE, the first row of the new matrix would equal (1∙2 + 3∙8) (1∙4 + 3∙10) (1∙6 + 3∙12), or (2 + 24) (4 + 30) (6 + 36). The second row of the new matrix DE would equal each element of the second row of the first matrix multiplied by each element of the column of the second matrix or (5∙2 + 7∙8) (5∙4 + 7∙10) (5∙6 + 7∙12) or (10 + 56) (20 + 70) (30 + 84). The new matrix would consist of the elements [26 34 42 66 90 114] in a 2 x 3 matrix. .
Figure 7: Matrix DE
Why Isn’t Multiplication of Matrices Commutative?
Suppose Matrix F consisted of the elements [1 2 3 4] in a 2 x 2 matrix and Matrix G consisted of the elements [ 0 1 3 5 7 9] in a 2 x 3 matrix.. The new Matrix FG would consist of the elements [10 15 21 20 31 44] in a 2 x 3 matrix. Matrix GF would be a 2 X3 matrix X a 2 X2 matrix, which would be undefined, as the number of columns in G (3) is not equal to the number of rows in F(2).
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in White Rock, BC, Canada: visit Tutoring in White Rock, BC, Canada