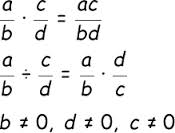Overview
Rational expressions may include constants or variables in the numerator and denominator. If the variable is in the denominator, values of the variable that cause the denominator to equal 0 must be excluded, because division by 0 is undefined.
Rational Expressions
Rational expressions can include variables or constants in the numerator or denominator. If both the numerator and denominator are constants, such as 2/3 or 13/15, they are familiar as fractions. Suppose the expression is x/3, or (x + 2)/(x + 13), or even (x2 + 18x + 81)/3(x + 9). Those are rational expressions.
Figure 1: Rational expressions can include variables or constants in the numerator or denominator.
Avoiding Zero Denominators
If the variable is in the denominator, values of the variable that cause the denominator to equal zero must be excluded. For example, suppose the expression is 2/x – 3. In this case, the value of x cannot equal 3, because 3 – 3 equals 0, and a rational expression 3/0 is undefined. If the expression is (3x3 + x2 + 10)/(x2 + 10x + 25), the value of x cannot equal -5.
Multiplying Rational Expressions
Multiplying rational expressions is similar to multiplying fractions. The difference is that either the numerator or the denominator or both may contain variables. Suppose the expression is (x – 2)/3 ∙ (x + 2)/(x + 7). The result will be [(x + 2)(x – 2)]/[3(x + 7)]. In this case, x cannot equal -7. It doesn’t really matter if x equals either 2 or -2, because the numerator can equal 0, just not the denominator.
Figure 2: Multiplying or dividing rational expressions in symbol form.
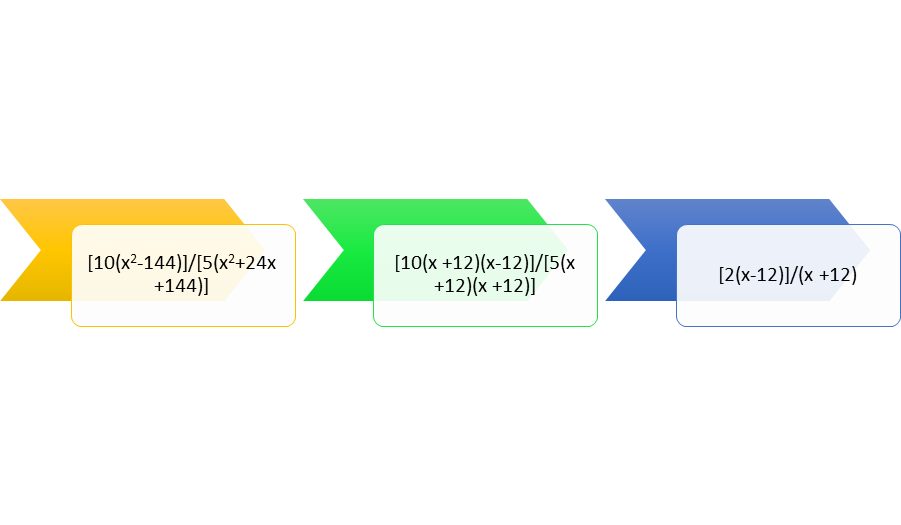
Simplifying Rational Expressions
In order to simply rational expressions, eliminate common factors that are both in the numerator and denominator. Suppose that the rational expression is 10(x2 – 144)/5(x2 + 24x + 144). It is often necessary to factor the expressions to see if anything can be eliminated. The numerator is 10(x + 12) (x – 12) and the denominator is 5(x + 12) (x + 12). The expression can be divided by [5(x +12)]/ [5(x +12)] to result in [2(x – 12)]/(x + 12). Similarly, suppose the multiplication is (x2-25)/6 ∙ 3/ (x + 5). The result will be [(x + 5) (x – 5)3]/ [6(x + 5)]. The expression can be divided by [3(x + 5]/[3(x + 5)] to result in a simplified (x – 5)/2.
Figure 3: Simplifying a rational expression by factoring.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Hope, AR: visit Tutoring in Hope, AR