Overview
Real numbers are the rational and irrational numbers that people deal with in everyday life. Hyperreal numbers include numbers that are infinitely large, infinitely small, or infinitesimal, along with the reals. Surreal numbers include the reals, the hyperreals, and other constructs in advanced mathematics that sometimes behave like numbers and sometimes do not.
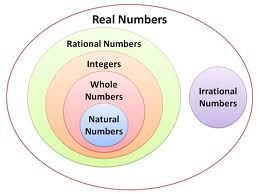
Rational Numbers
Real numbers include rational numbers, any number that can be expressed as a ratio, whether positive or negative. Rational numbers include the natural or counting numbers, such as 1, 2, 3, 4, and so on. The integers include negative numbers and zero, which is neither positive nor negative. Rational numbers can be plotted on a number line with the origin at zero.
Irrational Numbers
Irrational numbers are types of real numbers that cannot be expressed as an exact ratio. When they are represented by decimals, the decimal digits do not repeat, nor do they terminate in zeros. They are some of the most useful numbers, including pi π, tau τ, the natural logarithm e, and any root that is not an exact number, such as √2. The irrational numbers pi, tau, e, and others are transcendental and more numerous than rational numbers.
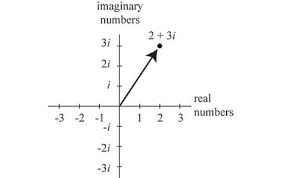
Complex Numbers
Rational and irrational numbers can be shown on a number line. Complex numbers can be shown on a number plane, at angles to the number line. They are used in special algebraic situations and take the form a + bi, where a and b are real parts of the number and the construct i equals the square root of -1. Since the imaginary part of a complex number can be equal to 0, all numbers are complex numbers. They are used in many applications, including chemistry, physics, and electrical engineering.
Hyperreal and Surreal Numbers
Hyperreal and surreal numbers are relatively new concepts mathematically. Hyperreal numbers include all the real numbers, the various transfinite numbers, as well as infinitesimal numbers, as close to zero as possible without being zero. They have applications in calculus. Surreal numbers include all the real, complex, hyperreal, transfinite, and infinitesimal numbers as well as some constructs that have applications in game theory. They may also have applications in computer processing.
Interested in pre-calculus tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Baltimore, MD: visit: Tutoring in Baltimore, MD