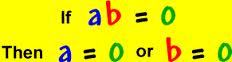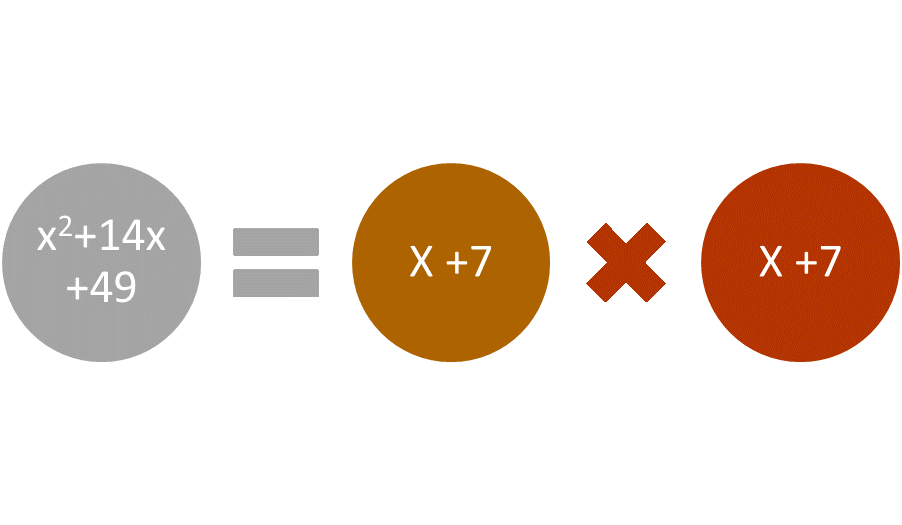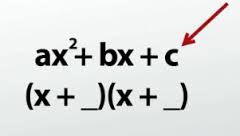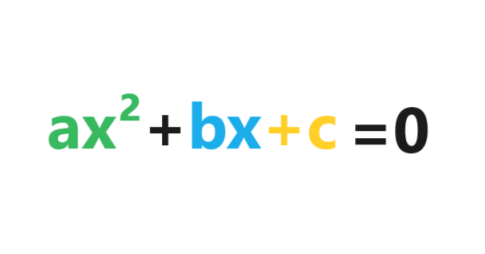Overview
Although the Quadratic Formula can be used to solve quadratic equations, or show that the equation has no solution, it is not always necessary to use it. Some quadratic equations can be solved right away by factoring, which is a much shorter and easier process.
The Zero Product Property
The Zero Product Property is a shortcut to solving equations such as 5(x – 3) = 0. Since 5 is not equal to 0, x – 3 must be equal to 0, so x is easily solved as 3. Suppose that the equation is 35t – 16t2 = 0. It can be further factored as t(35 – 16t) = 0. The variable t could have two possible solutions. Either t is equal to 0, or -16t is equal to -35, in which case 35/16 is equal to about 2.19. Factoring was a shortcut to solving the equation when it was already equal to 0.
Figure 1: The Zero Product Property
Perfect Square Trinomials
Some quadratic equations are perfect square trinomials. Suppose the equation were x2 + 14 x + 49 = 0. That could be factored easily as (x + 7) (x + 7) = 0. Then x must equal -7, because 7 – 7 equals 0. In order to check the problem, 14(-7) is -98, and 49 + 49 equals 98, and 98 – 98 = 0.
Figure 2: A perfect square trinomial can be factored easily
Easily Factored Trinomials
Although not every trinomial is a perfect square, many are factored almost as easily. Suppose the equation were x2 – 6x – 27 = 0. The x2 term has a coefficient of 1, so the pattern will be (x +) (x +). Similarly, the constant term is -27, so one of the factors must be negative. Since 3 times 9 is 27, 3 times -9 is -27. Also, -9x + 3x = -6x. Therefore, x could equal -3 or 9, according to the Zero Product Property.
Figure 3: An easily factored trinomial follows a pattern.
Common Monomial Factors
Sometimes trinomials have a common factor, and once that is factored out, the remaining quadratic factor can be factored still further, making it easy to solve. Suppose the equation is 4x3 – 18x2 + 8x = 0. Every term in the trinomial has a common factor of 2x, so it can be simplified as 2x(2x2 – 9x + 4). The trinomial can be further simplified to 2x(x – 4) (2x – 1) = 0. Using the Zero Product Property, if 2x equals 0, then x could equal 0. If x – 4 equals 0, then x could equal 4, and if 2x – 1 equals 0, then x could equal ½.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Ferndale, WA: visit Tutoring in Ferndale, WA