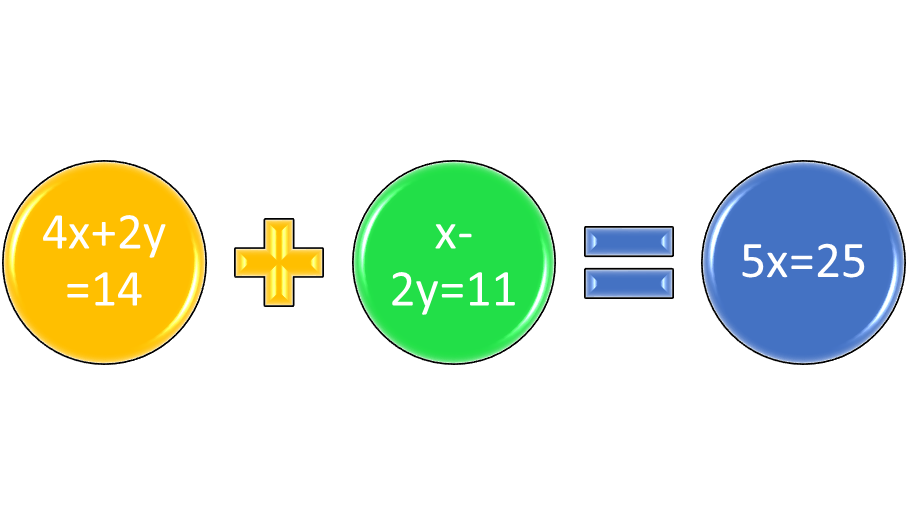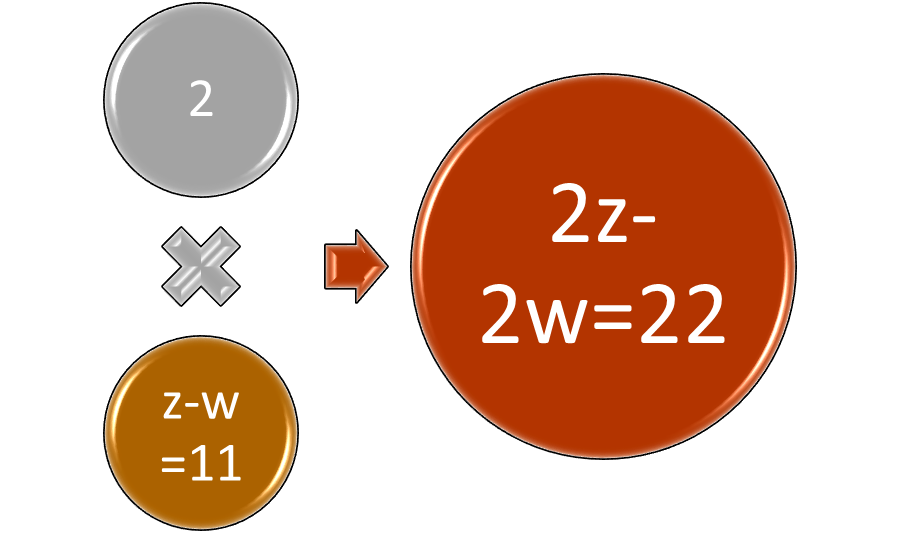Overview
Although systems of equations can be solved by substitution, there are situations where systems of equations can be solved by addition and multiplication. If the coefficients of one variable are opposite, they can be solved by addition, but sometimes the coefficients of one equation have to be multiplied by a constant in order for them to be opposite.
Putting Equations in Order
In order for systems to be added, they must first be arranged so that the variables are in the same order, to guard against inadvertent errors in operations. In order to use either addition or multiplication to solve systems, both equations should be in a form Ax + By = C. If one of them is in another form, the order must be changed first. Suppose that the systems in question are 4x + 2y = 14 and -2y +x = 11. The order of the second equation can be changed to x – 2y = 11 before the systems can be solved.
Using Addition to Solve Systems
The equations 4x + 2y = 14 and x – 2y =11 can be added using the rules for adding polynomials using like terms. The variables 4x + x are added as 5x, and 2y + -2y are 0. The constants 14 + 11 = 25. The new equation that results from adding them is 5x = 25. Solving for x, x = 5. Notice that adding these two systems cancels out the y variable, so the equation can be solved for x.
Figure 1: When solving systems using addition, one term (2y – 2y) should be cancelled so the other can be solved.
Using Substitution
Now that x is solved, it can be replaced in either equation to solve for y. So 20 + 2y = 14 means the same thing as 2y = 14 – 20, and 2y = -6, so y = -3. In order to check, use the second equation in the system, so that 5 + 6 = 11.
Using Multiplication to Solve Systems
In order to solve some systems of equations, multiplication by a constant must be used. This changes one of the equations into a usable form so that one variable can be temporarily canceled out, in order that one variable can be solved and substituted for another. Suppose the equations were 4z + 2w = 14 and z – w = 11. In order to solve the system, the order would not have to be changed, but the second equation would need to be multiplied by 2, so that 2(z – w) = 22. The new second equation is then 2z – 2w = 22. Using addition to solve systems, the equations would be 4z + 2w = 14 and 2z – 2w = 22. Adding like terms 4z + 2z is 6z, 2w – 2w is 0 and 14 + 22 is 36. The new equation is 6z = 36, so z = 6. Using substitution, 24 + 2w = 14 so 2w = 14 – 24, so w = -5. Checking with the second equation, 6 + 5 = 11, as –(-5) means the same thing as +5.
Figure 2: Multiplying one equation by a constant makes it possible to cancel like terms and solve the system.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Rockingham, VT: visit Tutoring in Rockingham, VT