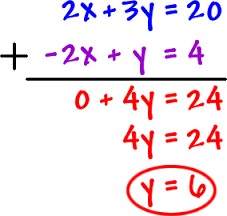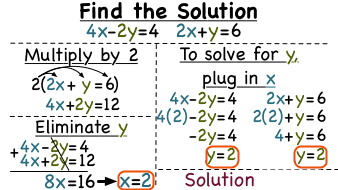Overview
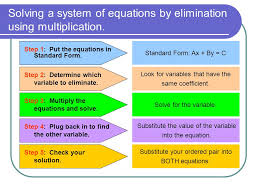
Besides solving systems of equations by graphing and substitution, systems of equations can also be solved by addition. Math students can choose the best method for the problem at hand. Sometimes this process is called “solving systems of equations by elimination”.
Using Addition
Although some systems of equations can be solved by substitution, other systems can be solved by adding both equations. Both equations must be written in standard form as Ax +By =C. For example, suppose the equations in the system are x +y = 5 and 2x –y = 4. They can be expressed as x +2x +y –y = 5 +4. Now x +2x equals 3x, y-y = 0, and 5 +4 = 9. The new equation is 3x +0 = 9, or x =3. If 3 +y = 5, then y equals 2. Checking the solution in the second equation, 2x or 6 -2 does equal 4. The addition method can be used because the addition property for equations states that we can add the same number to both sides of the equation, and the equations are still equivalent expressions, and make a true statement.
Using Multiplication, Then Addition
The multiplication property of equations is an extension of the addition property, since multiplication is repeated addition. Therefore, we can multiply each side of the equation by the same number or expression. This is especially useful to eliminate a variable, before using the addition method. For example, suppose the equations in a system were 5x +3y = 17 and 5x-2y =-3. If they were to be added without multiplying, the new equation would be 5x +5x +3y – 2y = 17-3, or 10x-y =14. That is not closer to a solution, as there are still 2 variables in the system. Suppose both sides of the second equation are multiplied by -1, so that the new equation is -1(5x -2y) = -1(-3), or -5x +2y = 3. Using the addition method, 5x – 5x +3y +2y = 17 +3, or 5y =20, or y =4. If 5x +12 = 17, then 5x = 5, or x =1. Using the second equation to check, 5-8 = -3.
Using Multiplication More than Once
Sometimes the multiplication property needs to be used more than once in order to use the addition method. Suppose the system of equations is 5x +3y = 2 and 3x +5y =-2. Using the multiplication property once, 5(5x +3y) = 5(2) = 25x +15y = 10. The second equation can be multiplied by -3, so that -3(3x +5y) = -3(-2), or -9x -15y =6. Then the addition method can be used, so that 25x -9x +15y -15y = 10+6 or 16x = 16, or x =1. Solving for y, 3y = 2-5, or -3, so y= -1. Checking the second equation, 3 (1) + 5 (-1) = -2. The solution is (1, -1).
Problem-Solving Using the Addition Method
Suppose that the problem were to translate a word problem to a system of equations, then solve. The sum of two numbers is 115, and their difference is 21. Understanding the problem, the first equation is x +y = 115, and the second equation is x-y = 21. Using the addition method, x + x +y-y = 115 +21, or 2x =136, or x = 68. Substituting for x, 68 +y = 115, or y = 47. Checking with the second equation, 68-47 = 21.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Huron, SD: visit: Tutoring in Huron, SD