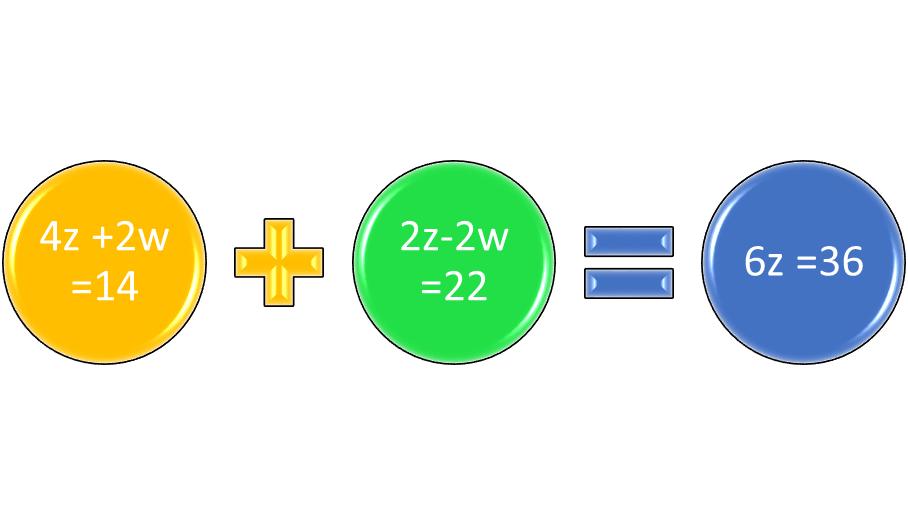Overview
One of the methods for solving systems of equations with two variables adds the equations together and then eliminates one variable. It is a useful strategy when solving by substitution would be too cumbersome.
Adding Systems of Equations
Entire systems of equations can be added just as easily as adding polynomials. Suppose one equation in the system is 2r + 3s = 13 and the other equation is 4r – 3s = 17. The 2r and 4r can be added to equal 6r and the 3s and -3s can be added to equal 0. Then 13 and 17 equal 30.
Figure 1: An example of the process of adding systems of equations.
Using the Additive Inverse
Note that the additive inverse of 3s is -3s, so 3s -3s equals zero. This is a very important key to the elimination method. Adding the equations together when one monomial is the additive inverse of the other eliminates that variable temporarily, so that 6r = 30. If 6r = 30, then r equals 5. If r equals 5, then 2r equals 10, and 10 + 3s = 13, 3s = 13 – 10 or 3 and s equals 1. To check the other equation, 4∙5 or 20 – 3 = 17.
Multiply Before Adding
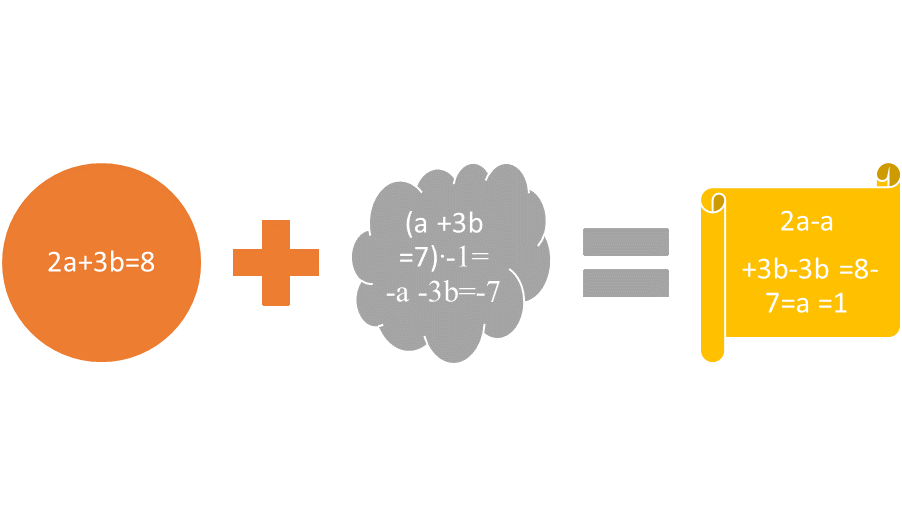
In the above example, the additive inverses were clearly stated as 3s and -3s. Sometimes, equations need to be multiplied by a constant to find an equivalent equation. Remember that the graphed lines of equivalent equations, such as x + y = 8, 2x +2 y =16, 3x + 3y = 36 and so on, are still the same line with the same solution set for x and y. Suppose the system of equations were 2a + 3b = 8, a + 3b = 7. The monomials 3b and 3b are not inverses of each other. In order to change 3b to its inverse, multiply every term in the equation by -1 so that the equivalent becomes –a – 3b = -7. 2a- a equals a, 3b – 3b = 0, and 8 – 7 = 1. If a equals 1, then 2 + 3b = 8, and 3b =8-2 =6 so b =2. Similarly, 1 + 6 = 7. Suppose that 3w + 6x = -6 and 5w – 2x = 14. Then 15w -6x = 42, multiplying each monomial term by 3. Adding 3w + 6x = -6 and 15w -6x =42 leaves 18w = 36. If w = 2, then 6 + 6x = -6, or 6x = -6 + -6, 6x = -12, so x = -2. Similarly, 10 + 4 = 14.
Figure 2: Multiplying by the constant -1 leads to an additive inverse that can eliminate one variable.
Systems with No Solution
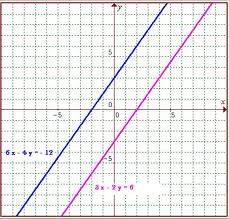
Just because systems can be added and then solved using substitution doesn’t mean that all systems of equations have a solution. Suppose the system of equations is x + y = 5 and 2x + 2y = 6. That leads to 2 equations x + y = 5 and x + y = 3, or y = 5 –x and y = 3 – x. If all terms in the equation x + y = 3 were multiplied by -1, then x – x + y – y = 5 – 3 leading to a false statement 0 = 2. If those linear equations were graphed on a coordinate plane, they would be parallel, showing no common solution.
Figure 3: Parallel linear equations in the coordinate plane have no common solution.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Hilton Head Island, SC: visit Tutoring in Hilton Head Island, SC