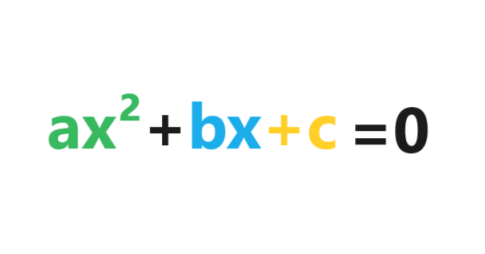Overview:
Solving quadratic equations is an important skill in algebra. Some methods of solving quadratic equations include factoring, taking the square root of both sides, completing the square, and using the quadratic formula. There are many applications where quadratic equations can be used, such as motion, time, distance, and speed.
What Is a Quadratic Equation?
A quadratic equation takes the form ax2 + bx + c = 0, where a, b, and c are all real numbers and the coefficient a is not equal to 0. It is also sometimes called a “second-degree equation” because the highest exponent is 2. Suppose the equation is 3x2 + 15x = -9. It can be changed to the standard form 3x2 + 15x + 9 = 0 by adding 9 to both sides. An equation such as 25x2 = 16 is also a quadratic equation. There is an a coefficient, no b coefficient, and it can be changed to standard form by subtracting 16 from both sides as 25x2 – 16 = 0.
Can the Equation Be Solved by Factoring?
Some quadratic equations can be solved by factoring. Suppose the equation were y2– 36 = 0. If y2is equal to 36, then y will equal the square root of 36 which is 6, or -6. Sometimes the equation can be solved by expanding the equation first. The equation y2– 36 = 0 can also be expanded to (y – √36)(y + √36) = 0, which has the same solution, y = ±6. Similarly, an equation such as (x – 6)2 = 64 can be solved by taking the square root of each side so that x – 6 = ±8. Solving x – 6 = 8, x = 14. Solving x -6 = -8, x = -2.
Can the Equation Be Solved by Completing the Square or the Quadratic Formula?
If an equation cannot be solved by factoring or taking the square root of both sides, it can be solved by completing the square. In a perfect square trinomial such as x2 + 6x + 9, the relationship between the coefficient of x and the 9 is that (1/2 ∙ 6)2 = 9. This principle can be used to solve other quadratic equations. Suppose that the equation were x2 + 6x + 8 = 0. This is not a perfect square trinomial (although it is close), but it can be solved by completing the square. First, if x2 + 6x = -8, then (1/2 ∙6)2 would equal the missing term if it were a perfect square trinomial. Substituting that number on both sides “completes the square”, so that x2 +6x +9 = -8 +9. Then it can be solved the rest of the way, so that x2 + 6x + 9 = 1. The complete square is then equal to (x +3)2 =1. Taking the square root of each side, x + 3 = 1 or x + 3 = -1 and can be solved as -2 or -4. Substituting the coefficients 1 (for a), 6 (for b) and 8 for c results in the same solution set for x, as (-6 ± √(36 – 32)/2 or (-6 ± 2)/2, which is equivalent to -8/2(-4) or -4/2(-2).
What Are Some Applications of Quadratic Equations?
Quadratic equations can be used in problems that involve upward motion or motion in more than one direction. For example, suppose a ball is thrown into the air from a hill 3 meters above the ground, at a velocity of 14 meters per second. The constant for gravity on the downward trip is 5x2so that the resulting equation is 5t2 – 14t – 3 = 0 which is a quadratic equation. Similarly, problems that involve triangles and use the Pythagorean Theorem can be solved using quadratic equations.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Kahului, HI: visit Tutoring in Kahului, HI