Overview
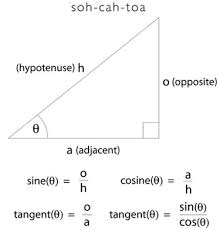
Right triangles have special properties that are important to determine trigonometric ratios, such as sine (sin), cosine (cos), tangent (tan), secant (sec), cosecant (csc), and cotangent (cot). Those ratios reflect the relationships between the opposite and adjacent angles of the right angle with the hypotenuse.
Trigonometric Ratios
Suppose a right triangle has an angle θ for one of the acute angles. The sine of θ (sin θ) is the ratio of the opposite side to the hypotenuse, the cosine of θ (cos θ) is the ratio of the adjacent side to the hypotenuse, and the tangent of θ (tan θ) is the ratio of the opposite side to the adjacent side. Those three ratios can be measured by the mnemonic SOHCAHTOA. There are three other trigonometric ratios that are the inverses of sine, cosine, and tangent. The inverse of sine is the secant, and the secant of θ (sec θ) is the ratio of the hypotenuse to the opposite side. The inverse of cosine is the cosecant, and the cosecant of θ (csc θ) is the ratio of the hypotenuse to the adjacent side. The inverse of tangent is the cotangent, and the cotangent of θ (cot θ) is the ratio of the adjacent side to the opposite side. These relationships can be determined from the Pythagorean Theorem.
Similar Right Triangles
All right triangles, regardless of size, are similar if they have angles that measure the same. Therefore, if one right triangle has an angle that measures θ, it will be similar to another right triangle that measures θ. The ratios sin, cos, tan, sec, csc, and cot will be the same for angle θ, no matter the length of the sides of the triangle.
Special Right Triangles
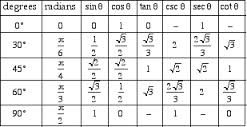
Some right triangles have special measures and ratios that can also be deduced from the Pythagorean Theorem. They are the 45-45-90 triangle (also known as the π/4, π/4, and π/2 in radian measure), and the 30-60-90 triangle (also known as π/6, π/4, and π/2). They can be used to calculate the trigonometric ratios.
Applications of Right Triangles
The principles behind right triangles and their ratios are used to calculate many different relationships, such as the height of a tree, a building, or a mountain, or the distance between the earth and the sun. A famous Greek geometer named Thales, who founded trigonometry, calculated the height of the Great Pyramid in Egypt, and Aristarchus estimated the distance from the earth to the sun.
Interested in trigonometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Las Vegas, NV: visit: Tutoring in Las Vegas, NV