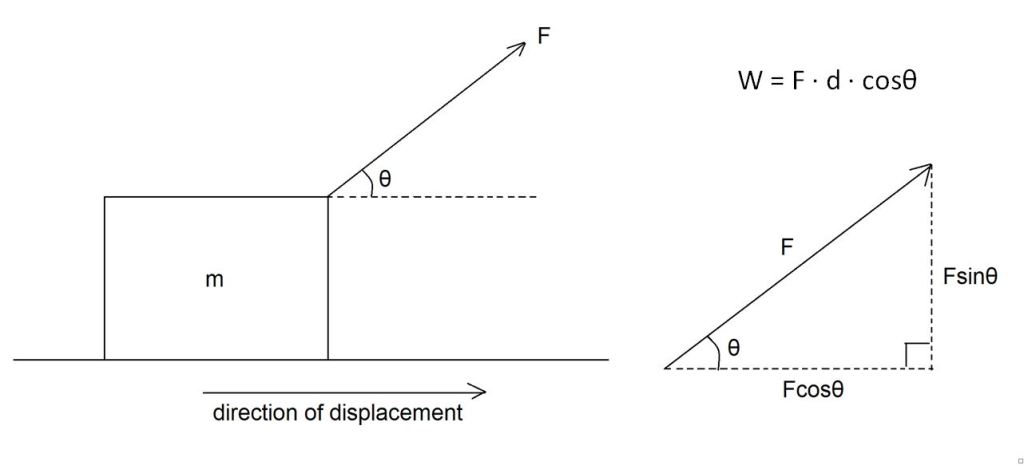
Work is the energy applied to an object as it moves some distance. The amount of work done is directly proportional to the magnitude of force applied, as well as the displacement of the object. In some cases, there may be an angle between the direction of displacement and force vector.
The force must be perpendicular to the direction of displacement in order to produce work. This can be considered through application of trigonometry, where the angle is found between the displacement distance and force vector. When the force opposes the direction of displacement, the work produced is negative.
Work is a scalar quantity as it does not have a defined direction. The unit for work is the Newton meter (Nm), since force is measured in Newtons (N) and displacement is measured in meters (m). Most commonly, work is written in units of joules (J), an SI unit. All types of energy, such as heat and potential energy, are measured in terms of joules.
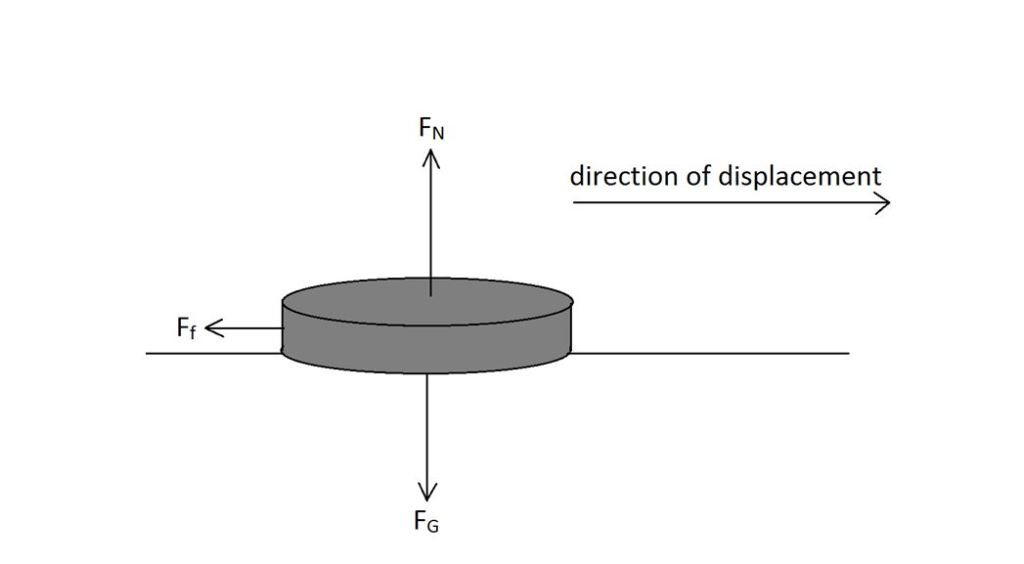
We can determine the work done by specific forces in varying scenarios. As a hockey puck slides across a surface, multiple forces are present and play separate roles. No work is done by the normal force or gravitational force since the vectors are perpendicular to the direction of displacement. On the other hand, the friction force is parallel to the surface, and does work on the hockey puck. However, the friction force produces negative work. This will always be the case as friction constantly opposes movement.
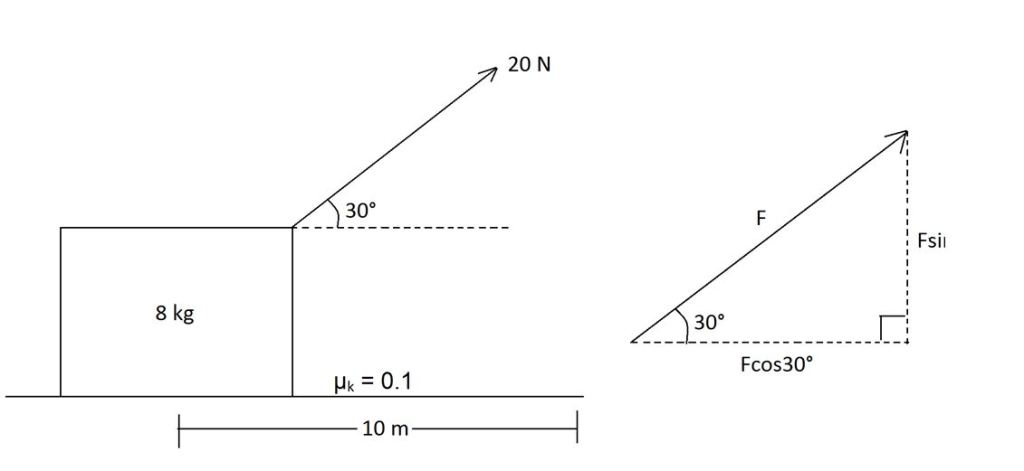
In the diagram above, an 8 kg crate is dragged 10 m across a wide room. The pulling force was applied with 20 N at a 30°angle. The coefficient of kinetic friction between the crate and carpeted floor is 0.1. What is the work done by each of the forces applied on the crate?
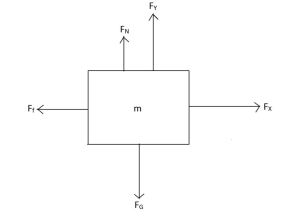
A free body diagram can be produced to show all forces acting on the crate. The applied force can be broken down to the x-component and y-component through trigonometry. Because they are parallel to the direction of movement, the x-component of the applied force and the friction force both produce work. The remaining forces are perpendicular and do not produce work.
| Work done by FX : | WFX = F ∙ d ∙ cosθWFX = 20 ∙ 10 ∙ cos30°WFX = 173.21 J |
| Work done by Ff : | WFf = Ff ∙ d ∙ cosω |
WFf = μk ∙ FN ∙ d ∙ cosω
WFf = μk ∙ (FG – FY) ∙ d ∙ cosω
WFf = μk ∙ (mg – Fsinθ) ∙ d ∙ cosω
WFf = 0.1 ∙ ((8 ∙ 9.81) – 20sin30°) ∙ 10 ∙ cos180°
WFf = – 68.48 J
The basic formula for work can be applied to both forces, although some forces may have to be broken down to simpler terms. The downward and upward forces are in equilibrium, and as a result, the normal force can be determined. The difference between the gravitational force and y-component of the applied force is equivalent to the normal force. The total work of the system can be determined through the sum of work values.
Wtotal = WFX + WFf
Wtotal = 173.21 J – 68.48 J
Wtotal = 104.73 J