Overview
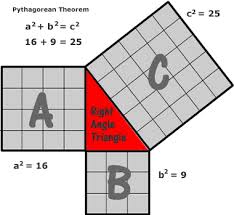
The relationship of the length of the legs of the right triangle to the hypotenuse is expressed by one of the most famous equations in geometry, the Pythagorean Theorem. Deriving the measurement of the sides of the right triangle was one of the earliest uses of irrational numbers.
Right Triangles
Right triangles have one 90-degree angle. The legs of the right triangle form the 90 degree angle, and the side opposite the 90-degree angle is the hypotenuse. The relationship between the lengths of the sides is given by the Pythagorean Theorem, a2 + b2 = c2. That means that if the length of the hypotenuse and one leg is known, the length of the other leg can be derived. Suppose that the length of the hypotenuse is 5 cm and one leg is 3 cm. Using the Pythagorean Theorem, 32 + b2 = 52, or 9 + b2 = 25. So 25 – 9 = b2, or 16 = b2. Taking the square root of both sides, b = 4 cm.
Figure 1: The Pythagorean Theorem.
Irrational Numbers
The followers of Pythagoras soon found that there was a big scar in the perfect geometric world. This was such a shock to them that they took out one Hippasus of Metapontum (who used irrational numbers) and drowned him at sea, or so the story goes. They couldn’t drown the idea so quietly, because the measurement of the side is not always a rational number. Suppose one leg of the triangle measures 10 feet and the other leg measures 15 feet. What is the length of the hypotenuse? 102 or 100 + 152 or 225 equals 325. The square root of 325 (in symbol form √325) is not a perfect square. It is a little more than 18, 18.03 to two decimal places.
Using Radicals to Measure Right Triangles
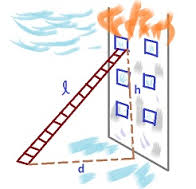
Right triangles are found all over, in the angle that a ladder makes with a building, the height of a tree, baseball diamonds and soccer fields. The applications of the Pythagorean Theorem and right triangles can be used to approximate and measure the lengths of the sides of these triangles. (Trigonometry is an entire branch of mathematics that gives more detail.) For example, suppose a ladder is 28 feet long. When the ladder is used against a building, it forms a right triangle. If the ladder is placed so the distance between the wall of the building and the base of the ladder is 2 feet, how high up will the ladder reach? One leg of the triangle is 2 feet, and the hypotenuse is 28 feet long. Using the Pythagorean Theorem, 22 + b2 = 282, or 4 + b2 = 784. If b2 = 784 – 4 = 780, then b = √780, or 27.93.
Figure 2: A ladder against the side of a burning building forms a real-life right triangle.
Right Triangles Made of Air
Sometimes the right triangle is actually an “air triangle”. The applications of the Pythagorean Theorem and radical expressions still hold. Suppose a plane is at a height of 5000 feet when it approaches an airport. At 5000 feet, the line of sight between the plane and the terminal is 38,000 feet. How far is the horizontal distance between the plane and the airport? This is truly an “air triangle”, as one leg of the triangle is the distance between the plane and the ground, or 5000 feet. Let that be a2. The line of sight between the plane and a point of ground at the terminal is the hypotenuse, or 38,000 feet. So 38000-5000 will be the other leg of the air triangle, or 33000. The square root of 33000 is 181.66.
Figure 3: Right triangles abound in the friendly skies.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Omaha, NE: visit Tutoring in Omaha, NE