Overview
Arithmetic sequences are sequences in which the difference between one term and the next term is a constant amount. They can be defined by developing a rule that relates that constant to the pattern.
Finding the Pattern
The first step in determining the sequence is to arrange the terms in order. Suppose there is a set of numbers such as {5, 11, 3, 9, 1, 7}. It is difficult to tell what kind of pattern there might be, because there isn’t any order to the terms. When they are ordered from smallest to largest, the pattern of numbers becomes more clear, {1, 3, 5, 7, 9, 11}. If there were more numbers in the set after 11, the largest number can be followed by three dots, called an ellipsis, so that the set would read {1, 3, 5, 7, 9, 11 …}.
Identifying the Sequence
If the pattern is an arithmetic sequence, it should be possible to find the constant difference between terms and predict the next three terms. For example, 1 +2 = 3, 3 +2 =5, 5 +2 =7, 7 +2 =9, 9 +2 =11. Following the pattern, the next three terms will be 11+2 = 13, 13 +2 = 15, 15 +2 = 17. However, if the pattern is not an arithmetic sequence, the difference between terms will not be a constant. Suppose the set were {1, 4, 9, 16…}. In that case, 1 +3 = 4, 4 +5 =9, 9 +7 = 16. If the pattern is recognized, the next three terms in the sequence are 16 + 9 = 25, 25 +11 = 36, 36 +13 = 49, but it is a different type of sequence.
Developing a Rule
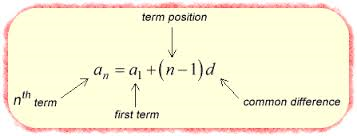
An arithmetic sequence can be translated into algebraic form by developing a rule to express the relationship between terms in the sequence. In the sequence {1, 3, 5, 7, 9, 11…}, the first term can be designated by the variable a1; the second term, a2; the third, a3, and so on. Therefore, a1 equals 1, a2 equals 3, a3 equals 5, and a4 equals 7. In order to get from the first term 1 to the second term 3, add the constant 2, also known as 1 + (1)2 = 3. In order to get from the first term 1 to the third term 5, add the constant 2 twice; or 1 +2(2) = 5. In order to get from the first term 1 to the fourth term 7, add the constant 2 three times, or 1 + (3)2 =7. Following the pattern, in order to get from the first term 1 to the nth term, add 1 to the constant 2(n-1) times, or an= 1+ (n-1)2.
Testing the Rule
In order to find if the rule works, substitute values for n in the algebraic formula. What is the 7th term in the sequence? According to the rule, a7 should equal 1 + (7-1)2, or 1 +12 = 13. Is 13 the 7th term? The sequence is {1, 3, 5, 7, 9, 11, 13}, so 13 is the 7th term. Similarly, the 13th term in the sequence should be 1 + 12(2), or 25, and the sequence is {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25}.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Omaha, NE: visit: Tutoring in Omaha, NE