Definition:
Similar triangles have equal corresponding angles and proportional sides.
There are three main methods to prove triangles are similar. The information provided in the question dictates which approach to attempt. Below are the details on each.
Side-Side-Side Similarity:
Use this method when the lengths of all three sides of both triangles are known . The goal is to show that the ratio between each pair of corresponding sides is equal. This is accomplished by creating and evaluating fractions out of the pairs of corresponding sides. When performing these calculations, there are two important things to note:
- It is important that only corresponding sides are compared. (ie. in a right angle triangle, the two hypotenuses would be compared in the fraction)
- The values in the numerator must all be from the same triangle; likewise the values in the denominator must all be from the same triangle.
If all of the ratios are the same, this means the sides are proportional, which is the definition of a similar triangle.
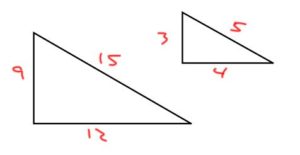
Ex: The following triangles are similar since
3 / 9 = 1 / 3
4 / 12 = 1 / 3
5 / 15 = 1 / 3
Angle-Angle Similarity:
Use this method when given:
- All of the angles in both triangles
- Information that allows you to solve for the angles
- Information that allows you to prove the angles in one triangle are congruent to the angles in the other triangle. (This will be the case when no numbers are provided in the problem)
The goal is to show that two of the angles are the same in each triangle. Because the sum of the interior angles of a triangle is always 180 degrees, knowing two of the angles are the same means we know the third angle must be the same as well. Note that some schools require this reasoning to be included with the proof as well. This means that if two of the angles in a triangle match two of the angles in the other triangle (equal corresponding angles), then the triangles are similar.
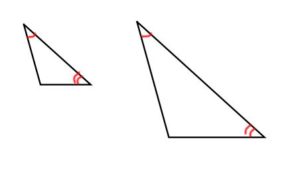
Ex: The following triangles are similar since it’s given that two of the angles in each triangle are the same.
Side-Angle-Side Similarity:
Use this method when presented with an “angle sandwich” in each triangle. This term refers to the situation where an angle, as well as the two sides surrounding it, are defined. If the angles apart of the “angle sandwich” are the same, check if the ratios between the two pairs of corresponding sides are equal (as described in side-side-side similarity above). Once this is proven to be true, it’s enough information to conclude that they’re similar triangles.
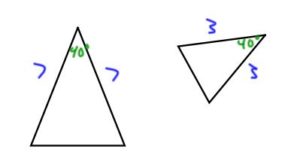
Ex: The following triangles are similar since the angles are equal and
3 / 7 = .43
3 / 7 = .43
If any of the above cases are false, then the triangles are not similar! Explaining why is an acceptable disproof.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Escondido, CA: visit: Tutoring in Escondido, CA.