Definitions:
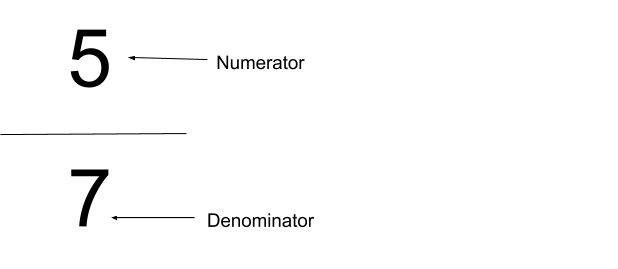
A rational function is defined as a function where both the numerator and denominator are polynomials.
A hole is a point where the function is undefined.
An asymptote is a line that continually approaches a given value but never reaches it.
When sketching a rational function, there are several characteristics that can be determined from the equation. Please note that it is important to factor both the numerator and denominator (if possible) before completing the following steps.
Holes (do this step first):
If both the numerator and denominator have a common factor, then the graph has a hole in it. To determine where the hole is, set the factor equal to zero and solve for x.
Ex. ((x + 2)(x + 3)(2x – 7)) / (x(x + 3)(x + 4)
There is a hole at x = -3 since (x + 3) is a common factor in both the numerator and denominator.
Asymptotes:
There are three kinds of asymptotes:
- Vertical: Use the denominator and the same method as when finding zeros from an already factored quadratic to find the values of the vertical asymptotes.
- Horizontal & Oblique :
- a) If the degree of the numerator is less than the degree of the denominator then there is a horizontal asymptote at y = 0
- b) If the degree of the numerator equals the degree of the denominator, then divide the leading coefficient of the numerator by the leading coefficient of the denominator to find the horizontal asymptote.
- c) If the degree of the numerator is exactly one degree greater than the degree of the denominator then there is an oblique asymptote. Using long division, divide the numerator by the denominator. The quotient is the equation of the oblique asymptote.
Ex. ((x + 2)(x + 3)(2x – 7)) / (x(x + 3)(x + 4)
The vertical asymptotes are at x = 0 and x = -4 since x and (x + 4) are both in the denominator.
There is a horizontal asymptote at y = 2 since both the numerator and denominator have the same degree (3) and the leading coefficient of the numerator is 2 and the leading coefficient of the denominator is 1.
Zeros/Roots/X-Intercepts:
Use the numerator and the same method as an already factored quadratic to find the zeros.
Ex. ((x + 2)(x + 3)(2x – 7)) / (x(x + 3)(x + 4)
The zeros are (-2, 0) (7/2, 0) since (x + 2) and (2x – 7) are both in the numerator.
Y-Intercept:
This is determined by subbing zero in for x and then evaluating the function. If there is a vertical asymptote at x = 0, there will be no y-intercept.
Ex. ((x + 2)(x + 3)(2x – 7)) / (x(x + 3)(x + 4)
There is no y-intercept since x = 0 is a vertical asymptote.
Below is a picture of ((x + 2)(x + 3)(2x – 7)) / (x(x + 3)(x + 4)
Please note that although there is a hole, it is not visible in this picture.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Madison, Wisconsin: visit: Tutoring in Madison, Wisconsin.