Overview
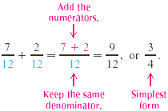
Adding and subtracting rational expressions with like denominators is similar to adding and subtracting fractions with like denominators. It is a three-step process: first add the numerators, then simplify the numerator, then simplify the result by factoring. Since subtraction is the inverse of addition, subtraction is a matter of adding the inverse of the numerator.
Adding with Variables in Common
Suppose the problem is 4x/5 + 6x/5. Since the numerators have a variable in common, 4x +6x can be added as 10x. Then (10x)/5 has the common factor of 5 in both the numerator and denominator. The simplified result is (2x)/1, or 2x. Suppose there were no variable in the expression. It would then be a fraction, so that 4/5 +6/5 would equal 10/5 or 2.
Adding with Variables in the Numerators and Denominator
Suppose the problem is (8y2)/(y +3) + (2y2)/(y+3). The numerators have variables, and so do the denominators. In this case, the denominator in each expression is the same, so the numerators can be added as 8y2 +2y2 =10y2. The expression is then (10y2/(y +3). There are no factors in common, so it is already in simplest terms.
Adding, then Factoring
Suppose the problem is (x2-4x-10)/(x-7) +(x-18)/(x-7). The denominator is the same for both rational expressions, so the numerators can be added. Combining like terms, (x2-4x+x -10 -18), the x2 is the only exponent. Then, -4x +x equals -3x, for the variables. Then, (-10 -18) equals -28, so the numerator is now (x2-3x-28), which can be factored as (x +4)(x-7). Using FOIL to check, x·x equals x2, 4x-7x equals -3x, and (-7·4) equals -28. The numerator [(x +4)(x-7)] can now be placed over the common denominator (x-7). The (x-7) in the numerator and denominator cancel out, so the answer in simplest terms is (x +4).
Subtraction with Like Denominators
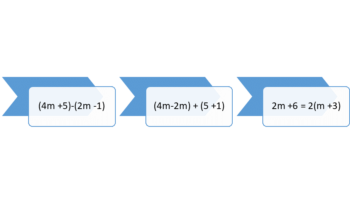
As subtraction is adding the inverse, the process is very similar to addition of rational expressions with like denominators. The numerator is subtracted, then the rational expression is simplified. For example, the first step to solve[(4m +5)/(m-1)] – [(2m-1)/(m-1)] is to combine the numerators as [(4m +5) –(2m -1)] or 4m-2m +5 +1 or 2m +6. The expression 2m +6 is not in simplest terms, as it can be factored as 2(m +3). Then using the common denominator, the entire solution is [2(m +3)]/(m-1).
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in St. Hyacinthe, QC, Canada: visit: Tutoring in St. Hyacinthe, QC