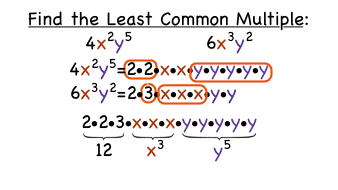Math Review of Adding Rational Expressions with Unlike Denominators

Overview

Adding rational expressions with unlike denominators is similar to adding fractions with unlike denominators.  The first step is to find the least common multiple (LCM) of the denominators.  This can then form the least common denominator.  Then multiply each rational expression so that it has the least common denominator.  Next, add the numerators now that the denominators are alike.  They can be factored and simplified.  Subtraction is the process of adding the inverse.

Finding the Least Common Multiple

To find the LCM of two or more algebraic expressions, first factor each expression.  Then, multiply all of the factors.  This is similar to finding the common factors of ordinary numbers without variables.  For example, the number 6 can be factored as 2·3, and the number 10 can be factored as 2·5.  Their least common multiple is 2·3·5 or 30.  Compare that to just multiplying 6·10, or 60.  The process is similar with expressions containing variables.  Suppose the expressions are 8x²y² and 12xy³.  The coefficient 8 can be factored as 2·2·2 and the coefficient 12 can be factored as 2·2·3.  The LCM of 8 and 12 can be factored as 2·2·2·3 or 24.  Similarly, the LCM of x² and x is x² and the LCM of y² and y³ is y³.  Putting them together, the LCM of 8x²y² and 12xy³ is 24x²y³.

Factoring Expressions

In order to find the LCM of polynomial expressions, it is also necessary to factor them first, if they can be factored.  Suppose one expression is y² +5y +4 and the other is y² +2y +1.  The first polynomial can be factored as (y +4) (y +1), and the second one can be factored as (y +1) (y +1).  The LCM is (y +4) (y+1) (y +1), or (y +1)²(y +4).  Expressions such as (t²+16) and (t-2) have no factors in common, so their LCM is (t²+16) (t-2).

Addition with Unlike Denominators

In order to add expressions with unlike denominators, first find the LCM of the denominators.  This can be used to form their LCD.  Then write each expression as an equivalent expression by multiplying it by a form of 1 using the LCD.  The numerators can then be added, and the rational expression can be simplified.  Suppose the expressions are (7x²)/6 and (3x)/16.    First, find the LCM of 6 and 16.  The number 6 factors as 2·3 and the number 16 factors as 2·2·2·2.  Their LCM will be 2·2·2·2·3 or 48.  The expression is [(7x²)/6] ·8/8, or (56x²)/48 + [(3x)/16] ·3/3 or (9x)/48.  Adding expressions over like denominators, the solution is then (56x² +9x)/48.

Subtraction with Unlike Denominators

Subtraction with unlike denominators is similar to addition with unlike denominators, with an additional step.  First, find the LCM of the unlike denominators to form the LCD.  Then write each expression as an equivalent expression by multiplying it by a form of 1 using the LCD.  Then, subtract the numerators and write the difference over the LCD. The resulting rational expression can then be simplified.  For example, the expression is [(y +2)/(y-4)]-[(y +1)/(y +4)].  First, multiply [(y +2)/(y-4)] by [(y+4)/(y+4)].  The numerator is then (y +2) (y +4).  Then multiply – [(y +1)/(y +4)] by [(y-4)/(y-4).  The numerator is then – [(y+1) (y-4)].  Both are multiplied by the LCM, so the new numerator is {[(y +2) (y +4)] – [(y+1)(y-4)]}.  Expanding the numerator, (y +2 )(y +4 equals y² +6y +8, and -[(y+1)(y-4)] equals –(y²-3y-4)  or -y² +3y +4, or y²-y² +6y +3y+8 +4 or (9y +12)/[(y +4)(y-4)] or 3(3y+4)/[(y +4)(y-4)].

Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Selma, AL: visit: Tutoring in Selma, AL