Overview
Many applied problems can be solved using rational equations and proportions. Some of the types of problems that can be solved include problems involving different rates of work, different rates of motion, proportions, or similar triangles.
Work Problems
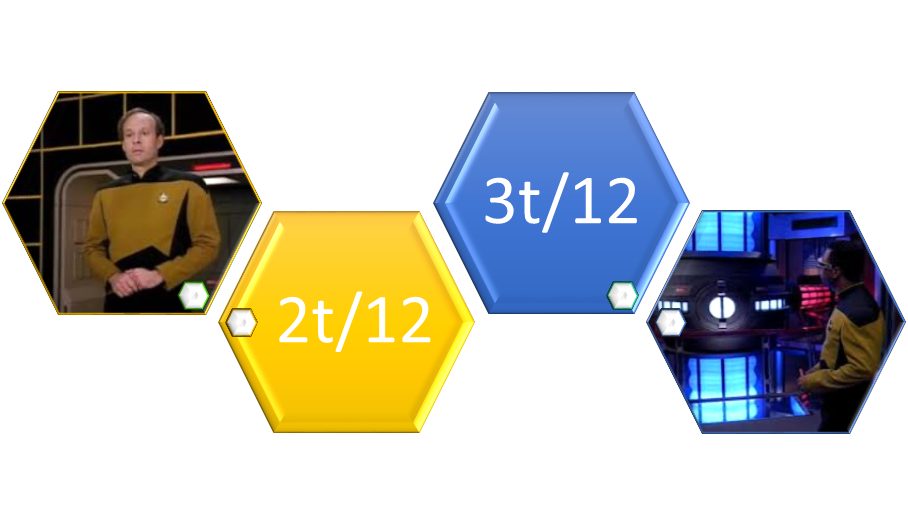
Many problems that involve rates of work are actually rational equations. Suppose that it takes Geordi 4 hours to realign the phase conduits and Barclay 6 hours to realign the phase conduits in the engine room of the Starship Enterprise. How long will it take them to do the job working together? Some fraction of 4, or, t/4, will be Geordi’s share of the work, and some fraction of 6, or t/6 will be Barclay’s share of the work, and both t/4 + t/6 will equal 1. Both fractions should be in like terms to add them, so 3t/12 +2t/12, or 5t/12 =1. Multiplying both sides by 12, 5t = 12, so t = 12/5 or 2 2/5 hours for the work in the engine room to be complete.
Figure 1: Work problems answer the question, When will the job be complete?
Motion Problems
Most motion problems involve some form of the relationship between distance, rate and time, such that distance = rate ∙ time. Suppose that a Vulcan sehlat can run 20 km faster than a Klingon targ. The Vulcan sehlat can run 7 km in the time it takes the Klingon targ to run 5 km. How fast can both run? There are 2 equations that can be solved in this system; 5=rt for the Klingon targ, and 7 = (r + 20) t for the Vulcan sehlat. Solving each equation for t means that t = 5/r for the targ, and t = 7/(r + 20) for the sehlat. Since the times are the same for both animals, 5/r =7/(r + 20). Unlike the work problem, there are no factors in common. In order to put both fractions in like terms and cancel the fractions in the denominator, both sides of the equation can be multiplied by r(r + 20). Therefore 5(r + 20) = 7r, or 5r + 100 = 7r, or 100 = 7r – 5r or 100 = 2r, or r = 50. The targ runs 50 km an hour and the sehlat runs 50 + 20, or 70 km an hour.
Proportion Problems
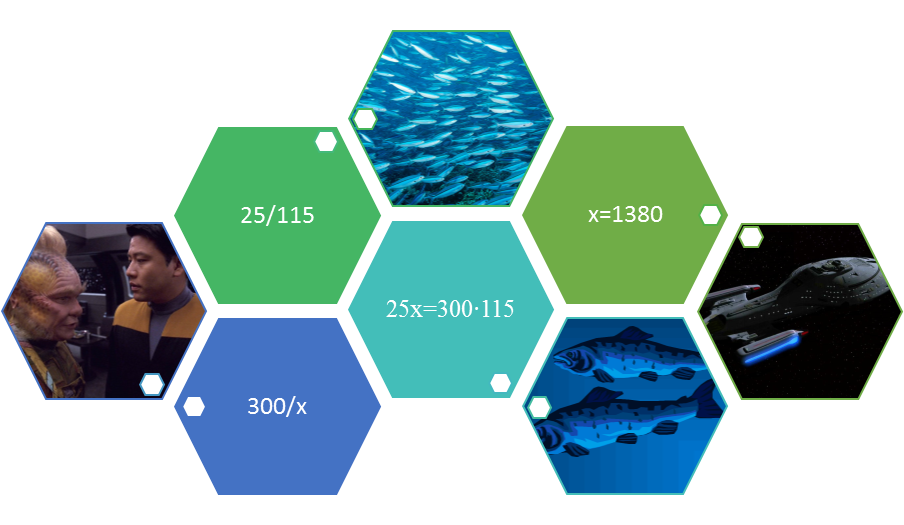
Problems that involve comparable proportions use rational equations. Voyager is running out of food supplies, so an away team goes to an uncharted system in the Delta Quadrant. Neelix finds a species of edible fish in a lake. He has no idea how many there might be in the lake and doesn’t want to disturb the ecology of the lake too much. Harry Kim has a plan. If 300 fish are tagged and then set free, the proportion of the tagged fish that are caught to the total number of fish caught will be roughly the same proportion as the 300 fish that were tagged to the total number of fish in the lake. Harry and Neelix together catch 115 fish and 25 of them are tagged. (Since all 115 are edible, they transport them back to the starship.) So 25 is to 115 as what proportion of 300? The problem can be set up as 25/115 = 300/x. In order to put both in like terms and cancel the fractions in the denominator both sides can be multiplied by 115x. This leaves 25x = 115∙300 = 34500, so x equals 1380.
Figure 2: Proportion problems use rational equations.
Similar Triangles
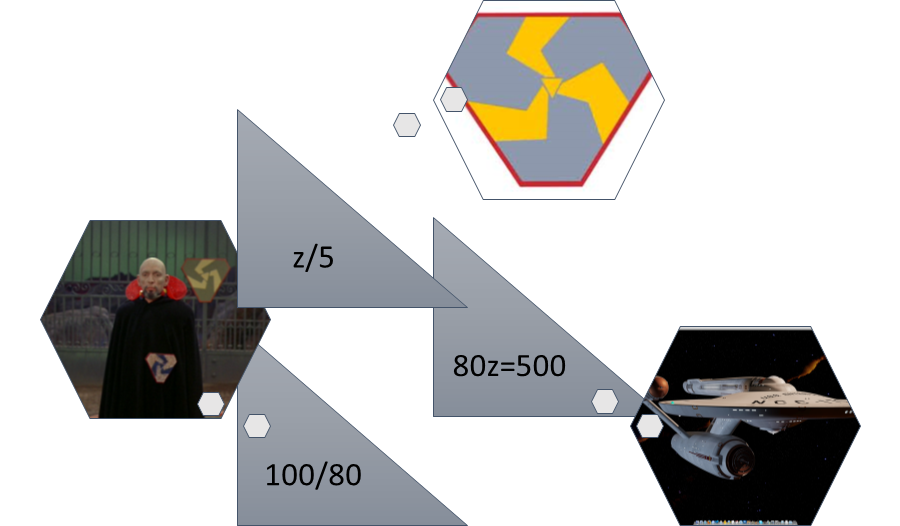
Similar triangles are triangles with corresponding angles equal and corresponding sides proportional. On the planet Triskelion, the triangle is often used as a symbol. Although Captain Kirk was too busy fighting for his life to notice, the triangular medallion that the overseer was wearing and the triangular arena where he was fighting were similar triangles. If the medallion had two sides with measurements z tries and 5 tries and the triangular arena had corresponding sides with measurements 100 tries and 80 tries, what was the measurement of the side of the medallion? This problem is also a proportion, z/5 = 100/80, or 80z = 500, so z = 6.25.
Figure 3: Proportions of similar triangles can be solved by using rational expressions.
Interested in geometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Burbank, CA: visit Tutoring in Burbank, CA