Overview
If two linear equations are solved, and their solution is graphed on a Cartesian coordinate plane, there are three possibilities. The lines may be the same, with all solutions in common. They may never intersect, with no solutions in common. They may intersect at only one point, with one solution in common.
Review of the Coordinate Plane
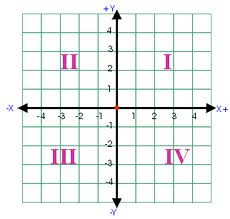
The coordinate plane is also called the Cartesian plane, in honor of the great mathematician Rene Descartes. It is one of the most familiar graphs in mathematics, with an x-axis and a y-axis, stretching out to infinity in all directions. The point where the x-axis and y-axis cross is called the origin. Its coordinates are (0, 0). It is divided into four quadrants. They are usually called I, II, III, and IV. In Quadrant I, values of x and values of y are positive. In Quadrant II, values of x are negative and values of y are positive. In Quadrant III, values of x and values of y are negative. In Quadrant IV, values of x are positive and values of y are negative.
Figure 1: The coordinate plane.
Equations with All Solutions in Common
If two or more equations have all solutions in common, the graph of their solutions will contain all solutions along the same line. In geometric terms, the points are collinear. It algebraic terms, the systems are dependent. Suppose the equations were x +y = 5 and 2x +2y =10. If x equals 1, then y equals 4; x equals 2, y equals 3, and so on. If the line for the equation x +y =5 is blue, and the graph of 2x + 2y = 10 is red, the lines will be superimposed, and the graphed collinear line is purple.
Equations with No Solutions in Common
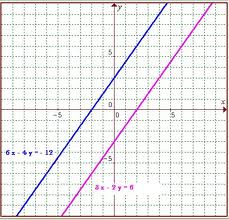
If two or more equations have no solutions in common, the graph of their solutions will contain all solutions along parallel lines. Suppose one equation is y = 3x + 2 and the other equation is y = 3x -1. The slope of each line is 2, so they have the same slope. The y-intercept of the first can be graphed vertical or perfectly horizontal have the same slope and different y-intercepts. Horizontal lines have a slope of zero by definition, but they each cross the y-axis at different points. Vertical lines have the same undefined slope, but they each cross the x-axis at different points.
Figure 2: When two linear equations have no solutions in common, their graphed lines are parallel.
Equations with One Point in Common
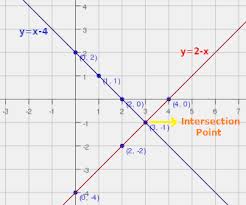
Many systems of linear equations have a single solution that satisfies both equations. When those linear equations are graphed, they intersect at a single point. The linear equations may meet at many different angles, either acute or obtuse. When they meet at a 90 degree perpendicular angle, the values that solve each equation are in definite relationship to one another. Suppose that the equation for Line 1 has a slope of m1 and the equation for Line 2 has a slope of m2. The product of m1 and m2 is -1. Similarly, if one equation can be graphed in a horizontal line parallel to the x axis, with slope 0, and the other equation in a vertical line parallel to the y axis, with undefined slope, the lines meet at one perpendicular point, a singular solution.
Figure 3: If a single solution satisfies both equations in a system, their graphed lines will meet at a single point.
Figure 4: The graphed lines will be perpendicular if the equations meet at a single point and the product of their slopes is -1.
Interested in geometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Carson City, NV: visit Tutoring in Carson City, NV