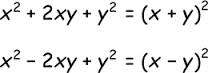Overview
When the a term has a coefficient of 1, polynomials can be factored into the form (a +b) (a +c) without worrying about its effect. However, if that a term has a coefficient not equal to 1, the coefficient must be considered when the polynomial is factored.
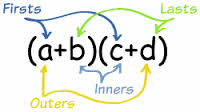
Review of FOIL
Suppose (x + 2) (x + 3) is multiplied. The First terms, x ∙x, become x2. The Outer terms, 3x, are next, then the inner terms, 2x. The last terms 2∙3, equal 6. When the polynomial is put in order, it follows the FOIL pattern of x2 + 2x + 3x + 6, or x2 + 5x + 6. (It follows the pattern of x2 + bx + c.) Because x2 is equal to 1∙ x2 in that case, the FOIL method can still be used. It just takes more attention to factor the expression.
Common Factors
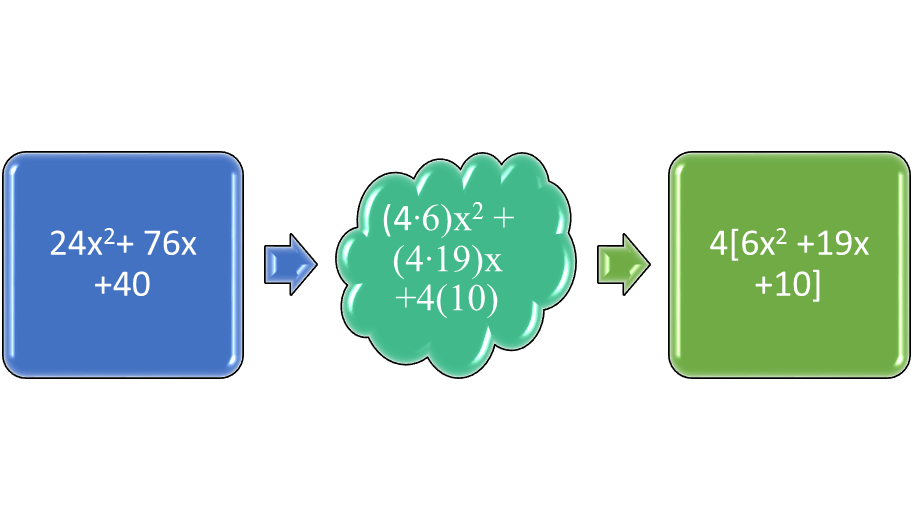
Factor out the largest common factor if that a term is not equal to 1 before using FOIL to do the rest. Suppose the polynomial is 5x2 + 15x + 125. The largest common factor is 5 in all the terms. Before using FOIL, the trinomial can be partially factored as 5(x2 + 10x + 25). Then it can be factored the rest of the way as 5(x + 5) (x + 5). Suppose that the trinomial is 24x2 + 76x + 40. The common factor of 4 can be factored out to leave 4(6x2 + 19x + 10).
UnFOILing the FOIL
In the above example, 6x2 + 19x + 10, the a term is equal to 6. Therefore, the two First terms will have a product of 6x2. They could be x and 6x or 2x and 3x, as x∙ 6x = 6x2, and 2x∙3x is also 6x2. The two Last terms will have a product of 10, so they could be 5∙2; 2∙5; 1∙10; or 10∙1. Then use trial and error to determine which Outer and Inner terms will have a sum of 19, the b term. Suppose the first combination is (x +5) (6x + 2). Using FOIL, the multiplication will result in 6x2 + 2x +30x +10. The 6x2 is correct, and the 10, but the middle term, 32x, is too large. What about (x +2) (6x +5)? The only terms to try are 5x + 12x, which is 17x, too small. Similarly, (x + 1) (6x + 10) results in a middle term of 16x, smaller still; and (x + 10) (6x + 1); 61x. Next, (2x + 1) (3x + 10). The sum of the middle terms is 23x, still too large; and (2x + 10) (3x + 1); 36x. Next, (2x + 2) (3x + 5), 16x again. That leaves (2x + 5) (3x + 2); 19x.
Reading the Signs
Whatever the value is of a, the sign within the factored terms matter. Suppose the trinomial is of the form ax2 +bx +c. It will factor as two additions in (x + p) (x + q). If the trinomial is in the form ax2 –bx +c, it will factor as two subtractions (x – p) (x – q). If the last term is negative, as in ax2 +bx –c or ax2 –bx –c, it will factor as either (x + p) (x – q) or (x – p) (x + q). If the middle term is positive, then p is less than q, and (x + p) (x – q) is the correct choice. If the middle term is negative, then q is less than p and (x – p) (x + q) is the correct choice.
Figure 3: The direction of the signs matter.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Klamath Falls, OR: visit Tutoring in Klamath Falls, OR