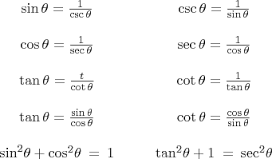Overview
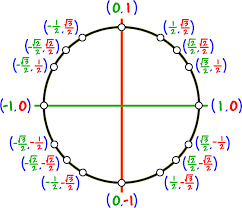
The unit circle has as its center the origin point of the Cartesian coordinates x and y, and has a radius 1. The trigonometric functions are also called circular functions, because they describe relationships between angles on the unit circle. We use different ways to describe trigonometry in order to see how the relationships and equations apply to different situations.
Special Values of the Trigonometric Functions
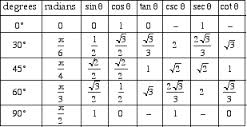
When the trigonometric functions are defined as circular, the special values of trigonometric functions can be seen on the unit circle. If t, the length of the arc from the coordinates (1, 0) equals 0, then sin t equals 0, cos t equals 1, and tangent t equals 0. This is because sin t equals y, cos t equals x, and tan t equals y/x. When t equals 0, y/x equals 0/1. If t equals π/4, then its coordinates are ([√2]/2, [√2]/2). Therefore, sin t is (√2)/2, cos t is (√2)/2, and tangent t is 1.
Domains of the Trigonometric Functions
If a circular function results in division by zero, it is undefined. Therefore, each function has a specific domain. Sines and cosines are defined for all real values of t. Tangents and secants are defined for all real numbers, except when the value of x is 0. This happens when the value of t equals (π/2) + nπ. Similarly, cosecants (csc) and cotangents (cot), are defined for all real numbers other than nπ, which happens when x equals 0.
Sign of the Trigonometric Functions
All other values of the trigonometric functions can also be seen on the unit circle. The unit circle is divided into quadrants by the Cartesian coordinates, so the signs of each circular function can be determined by the value of t. If the value of t has a positive value for both x and y, then it lies in Quadrant I. In Quadrant II, only the value of y is positive, and x has a negative value, so sin t and cosecant t will be positive. All other functions will be negative. In Quadrant III, both coordinates for x and y are negative. This means that tangents and their reciprocal cotangents will be positive. In Quadrant 4, x is positive and y is negative, so cosines and their reciprocal, secants, will be positive. There are several ways to remember the direction of the signs.
Fundamental Identities
The trigonometric functions are related to one another because the formula for the unit circle is x2+ y2=1. Therefore, the cosecant of t (csc t) is defined as 1/sin t; the secant of t (sec t) as 1/cos t, and the cotangent of t (cot t) as 1/tan t. Similarly, sin2t + cos2t = 1, tan2t +1 = sec2t, and 1 + cot2t = csc2t.
Interested in trigonometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Independence, MO: visit: Tutoring in Independence, MO