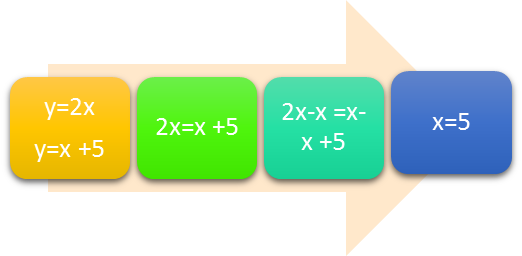Overview
Systems of linear equations can be solved by other methods than graphing, such as substitution and elimination. When solving by elimination, some systems can be solved by addition, subtraction, and multiplication.
Solving Equations by Substitution
Some systems of linear equations can be solved by solving first for one variable and then substituting that value in the system to solve for the other variable. Suppose that the equations in the system are y=2x and y = x +5. Both equations in the system have already been written in terms of y. Then, substitute the value 2x for y in the second equation to read 2x = x +5. Subtract x from both sides of the equation, so that 2x-x = x-x +5. Then x is equal to 5. If y = 2(5), then y equals 10 in the first equation. In the second equation, 10 = 5 +5. The ordered pair that solves the system is (5, 10).
Another Example
Suppose the equations in the system were 2x +y = 5 and y = x -4. The second equation is written in terms of y, so it can be substituted as 2x +x -4 =5 or 3x -4 =5 or 3x -4 +4 = 5 +4 or 3x =9. Dividing both sides by 3, 3x/3 = 9/3, or x =3. Therefore, 6 +y = 5, and y = 3-4. If y = 3-4, y equals -1 in the second equation. The variable y also equals -1 in the first equation, as 6-1 equals 5.
Solving Systems by Elimination
When solving systems of equations by elimination, both equations in the system are added. Equations are balanced so that one variable is eliminated. Two additional steps happen before the value of one variable can be substituted to solve the other. Like terms are aligned, so that one variable can be eliminated. Always, check the values of the variables in both equations to make sure that the solution is correct, because both equations in a system must be solved for the solution to be correct. Suppose that the equations in the system are x-2y= -19 and 5x +2y = 1. The like terms are already aligned, so that x +5x +2y -2y = -19 +1. Then 6x =-18 because the y values are cancelled out. The value of 6x/6 = -18/6, or x = -3. Then, substitute -3 -2y = -19 or -2y = -16, or y = 8. Similarly, 5(-3) + 2(8) =1.
Another Example Using Multiplication
Suppose that the equations are 2x +y = 3 and –x +3y =-12. Even though the like terms are aligned, one variable cannot be eliminated in one step when the equations are added. Both sides of an equation must be multiplied by a constant before the equations can be added, such that 2(-x +3y =-12) equals -2x +6y =-24. Combining the equations then leaves 2x-2x +y + 6y =3-24. Then 7y = -21 or y =-3. If 2x -3 equals 3, then 2x =6 and x equals 3, and -3 + -9 = -12.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Madison, WI: visit: Tutoring in Madison, WI