Overview
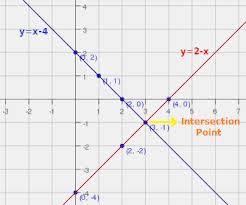
Parallel lines never intersect when they are graphed on the same plane, while perpendicular lines are lines that intersect at one point at right angles to each other. Their linear equations have special relationships.
Parallel Lines
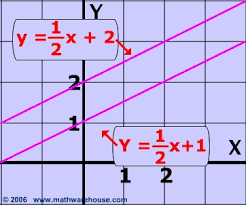
Parallel lines are lines in the same plane that have no points in common. Suppose that one line has the equation y = 2x. In slope-intercept form, its slope would be 2 and the y-intercept would be 0. Suppose that another line in the same plane has the equation y = 2x +4. In that case, its slope is still 2 but the y-intercept is 4. Those lines would have no points in common, because there isn’t any point that would be a solution of both equations. Therefore the lines would not intersect, and they are parallel.
Solving Equations for Parallel Lines
In the example of y=2x and y=2x +4, both lines have the same slope, 2, and the y-intercepts are different. Both equations are already solved for y. Given pairs of equations, they can both be put in slope-intercept form and solved for y to determine the slope and the y-intercept. If the slopes of the lines are equal and the y-intercepts are not the same, the lines are parallel. Suppose the equations for the lines are y = -3x +4 and 6x +2y = -10. Are those lines parallel? The slope of the line y = -3x +4 is already -3 and the y intercept is +4. Solving the second equation for y takes place in 2 steps, because 2y = -6x -10, moving the 6x, so y equals (-6/2) x – (10/2), or -3x -5. The slope of both lines is -3 but the y-intercepts are different, so they are parallel.
Perpendicular Lines
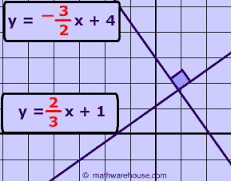
Perpendicular lines are lines that are in the same plane that intersect at one point, forming a 90° angle (a right angle). Slopes that have a product of -1 are perpendicular. Suppose a line has the equation y = 2x -3 and another line has the equation y = ( -1/2) x -4. The product of the slopes, 2(-1/2) is -1, so they are perpendicular.
Solving Equations for Perpendicular Lines
In order to determine of two equations are for perpendicular lines, solve for y and determine the product of the slopes. Suppose the equations are 3y = 9x +3 and 6y +2x =6 are perpendicular. Solving for y, 3y=9x +3 can be simplified to y = 3x +1 by dividing both sides by 3. Solving for y, 6y = -2x +6, or y = (-1/3) x +1. The product of the slopes, 3 (-1/3) = -1.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Providence, RI: visit: Tutoring in Providence, RI