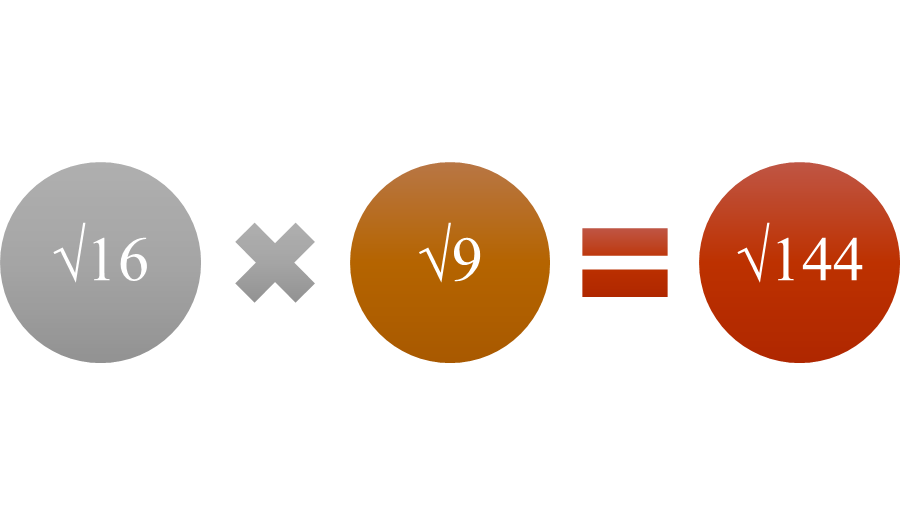Math Review of Multiplying and Simplifying Radical Expressions

Overview

Radical expressions contain one or more radicands, or expressions underneath root signs. They can be multiplied following rules for non-negative real numbers.

Radical Expressions

Radical expressions that do not have variables, such as √9 or √25 or even 6√5 are already familiar.  The radicand can also be a monomial, such as √(9x²) or over a polynomial, such as √(x² + 14x + 49).  Suppose the radical expression were √64.  The equivalent is the number 8, because 8 is the square root of 64.  Similarly, if the expression contained a variable, such as √x⁴, its equivalent would be x², because x² is the square root of x⁴.

Figure 1:  The radicand can be a monomial.

Multiplying Radical Expressions

Radical expressions can be multiplied as long as they are non-negative real numbers.  In symbol form, √a ∙ √b equals √ab.  For example, √16 ∙ √25 is the same thing as √ (16 ∙ 25) or √400.  This can be checked because √16 equals 4 and √25 equals 5 and 4 times 5 is 20, the square root of 400.  Similarly, √81 ∙ √x⁶ equals √ (81x⁶) or 9x³ because √81 is 9 and √x⁶ is x³, and 9 times x³ equals 9x³. Also, √(x + 2) ∙ √(x – 2) equals √(x + 2)(x – 2) or √(x² – 4).

Factoring Radical Expressions

Factoring radical expressions is also possible as long as the numbers are non-negative real numbers, such that √ab equals √a ∙ √b.  For example, √(100a¹⁰) is the same thing as √100 ∙ √a¹⁰.  Similarly, √(x² – 12x + 36) is the same thing as √(x – 6)(x – 6).

Simplifying Radical Expressions

Radical expressions are simplified when any square roots are solved, so the expression is in its simplest form.  For example, √(100a¹⁸) can be simplified as 10a⁹ because both factors are perfect squares.  The square root of a¹⁸ is a⁹, using the rules of exponents, because a¹⁸ = a^{9 + 9}.  Similarly, √(b² +22b + 121) can be simplified to (b + 11) because (b + 11)(b + 11) equals b² + 22b + 121. However, √(x² – 4) is already in its simplest form, as it is factored to √(x + 2)(x – 2).  The sum of square roots is not the same thing as the product of square roots.  For example, √(16 + 9) equals √25 which is 5.  However, the square root of 16 is 4 and the square root of 9 is 3 is 7, and 7 does not equal 5.

Figure 3:  The sum of square roots is not the same thing as the product of square roots.

Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.

SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Ketchikan, AK: visit Tutoring in Ketchikan, AK