Overview
Finding integrals, or integration, is the opposite of finding the derivative in calculus. The concept is closely connected with functions, and was independently discussed by both Newton and Leibniz in the Fundamental Theorem of Calculus.
Review of Functions
Suppose the values of x are {1, 2, 3, 4, 5} using set notation, and the function rule is [x +1 =y]. The values of y are {2, 3, 4, 5, 6}, because f(1) is 2, f(2) is 3, f(3) is 4, f(4) is 5, and f(5) is 6. In math language f(x) = x +1. Every value of x (the independent variable) has a corresponding value of y (the dependent variable). That simple function is linear, but functions can take many shapes, depending on the equation or inequality that describes them. A graphed curve is a function if and only if a vertical line intersects it in only one place.
Infinitesimals
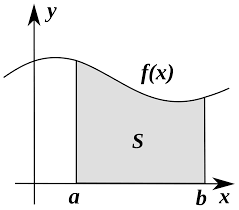
Mathematicians used the theory of infinitesimals and the vertical line test to find approximate values of the area under a curve before calculus was invented. (Derivatives measure the rate of change of the curve itself). The closer the approximation, the smaller the slices used. Suppose the area under the curve were measured by slices of 1 unit wide. Some of the units would overshoot the curve and add more area, while others would undershoot the curve and leave the area not measured. If the slices were made smaller, ½ unit, the measurement would be more accurate. The slices could be made smaller still until there were an infinite amount of slices that almost touched the curve. Then the measurement of the area under the curve would be the most accurate possible.
Integrals and Integral Notation
Newton and Leibniz arrived at a theory that brought together all of the rules and systems to deal with systems that were not linear. They laid the foundations for a new mathematical theory called calculus. The Fundamental Theorem of Calculus shows how integrals and differentials are related. Sir Isaac Newton developed calculus to account for the laws of motion and physics, while Gottfried Leibniz developed calculus to account for observations of how integrals and differentials worked. He paid close attention to symbolic meaning, and the symbols he defined are in common use.
Applications of Integrals
As scientists and engineers required more precise calculations, the methods of calculus became more useful. The continuous variation of light intensity in optics, the energy output of a steam engine, the reaction rate of chemicals all required calculus during the Industrial Revolution. Integrals figure in atomic reactions and the behavior of distant galaxies, the trajectory of a thrown ball and of a rocket carrying an orbital satellite.
Interested in pre-calculus tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Augusta, ME: visit: Tutoring in Augusta, ME