Overview
One of the methods of measuring angles is to measure them in relationship to a unit circle and as the measurement of an arc. Applications include periodic behavior such as light, sound or other waves along the electronic spectrum, and the processing of signals.
The Unit Circle
Suppose that a circle is constructed from a central point at the origin of the xy plane so that it has a radius of 1 unit. The equation for the unit circle is x2 + y2 = 1., which means that no matter what real numbers are chosen as values for x and y, they will fall at a particular point on the circumference of the circle, as long as the numbers satisfy the equation.
Terminal Points
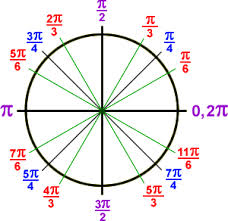
On the unit circle the origin is on values (0, 0); the circumference crosses the y axis at 2 points (1, 0; -1, 0); and the x axis at 2 points (0, 1; 0,-1). Any point P along the circumference can be measured by its distance t on the unit circle. The distance t is a real number. For values of t that are greater than 0, movement is counterclockwise from (1, 0), and for values of t that are less than 0, movement is clockwise from (1, 0). A full circumference of the circle is 2π (or tau τ).
Arcs around the Unit Circle
Another way of looking at terminal points around the unit circle is that the distance t is a real number that is the same as an arc. Therefore, a full arc is once around the circle (2π or τ), a half-arc is halfway around the circle. Different values of t are represented by the same terminal point.
Quadrants and Reference Numbers
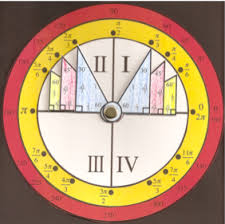
Still another way to look at a terminal point on the unit circle is by using the same general description of its location as any other point on the coordinate plane. A reference number is the shortest distance along the circumference of a circle between the terminal point t and the x axis. They are used as a shortcut to find the coordinates of the terminal point and the quadrant where it lies. Thus a terminal point with a positive value for x and a positive value for y will lie in Quadrant I; a negative value for x and a positive value for y, Quadrant II; a negative value for both x and y, Quadrant III; and a positive value for x and a negative value for y, Quadrant IV.
Interested in pre-calculus tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Mankato, MN: visit: Tutoring in Mankato, MN