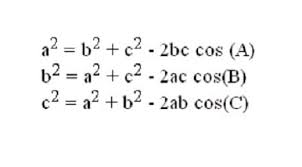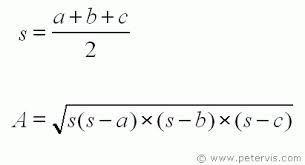Overview
The Law of Cosines is true because of properties of any triangle, not just right triangles. In fact, the Pythagorean Theorem is a special case of the Law of Cosines. The Law of Cosines and the Law of Sines can be used together to solve triangles with trigonometric ratios, if enough facts are known about them.
More Properties of Triangles
Any triangle has 6 pieces of information, covered by the three angles A, B, and C, and the lengths of the three opposite sides of the triangle a, b, c. By convention, side a is opposite angle A, side b is opposite angle B, and side C is opposite angle B. Also, the angles of any triangle add up to 180o, so if the measure of any two angles can be known or deduced from other properties of the figure, the measure of the third can be solved.
The Law of Cosines
The Law of Cosines in words states that the squared measurement of any side of a triangle equals the sum of the squared measurement of the other two sides minus twice the product of their measurement multiplied by the cosine of that included angle. In math language, that means 3 separate equations: a2= b2+c2— 2bc cos A; b2= a2+c2—2ac cos B; and c2= a2+ b2—2ab cos C. Suppose that angle C is a right angle. Then, cos C is 0, and the equation becomes the Pythagorean Theorem a2 + b2= c2.
Side-Angle-Side and Side-Side-Side
If the only three pieces of information that are known about a triangle are 2 of the sides and the angle between them, the Law of Cosines can be used to calculate one angle, and the Law of Sines can be used to calculate the other. In another application of the Law of Cosines, the angles of a triangle can be calculated if the measure of all three sides are known. That is because the longest side is opposite the largest angle, and the shortest side is opposite the smallest angle. The angles cannot be calculated using the measure of the sides alone by using the Law of Sines.
The Area of a Triangle Revisited
The area of a triangle can be calculated by at least three different formulas, two of them using trigonometric functions. The most familiar formula is A =1/2 bh; or the area of a triangle A equals ½ the base times the height of the triangle. If there is the measure of an angle θ, the formula for area A becomes A =1/2 ab sin θ, where the measure of both sides a and b for included angle θ are all known. If the measure of all sides are known, the formula for the area of a triangle is the square root of the semiperimeter s (half the perimeter) times (s –a) (s-b) (s-c).
Interested in trigonometry tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Portales, NM: visit: Tutoring in Portales, NM