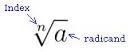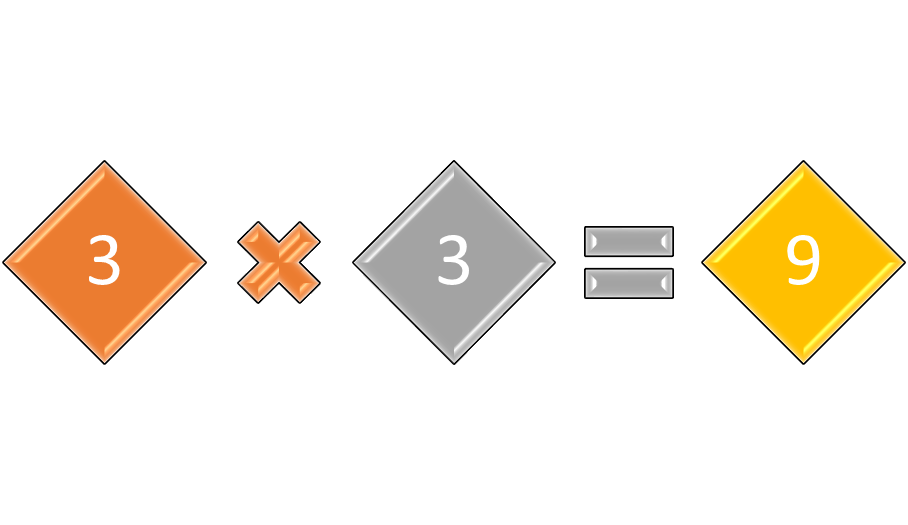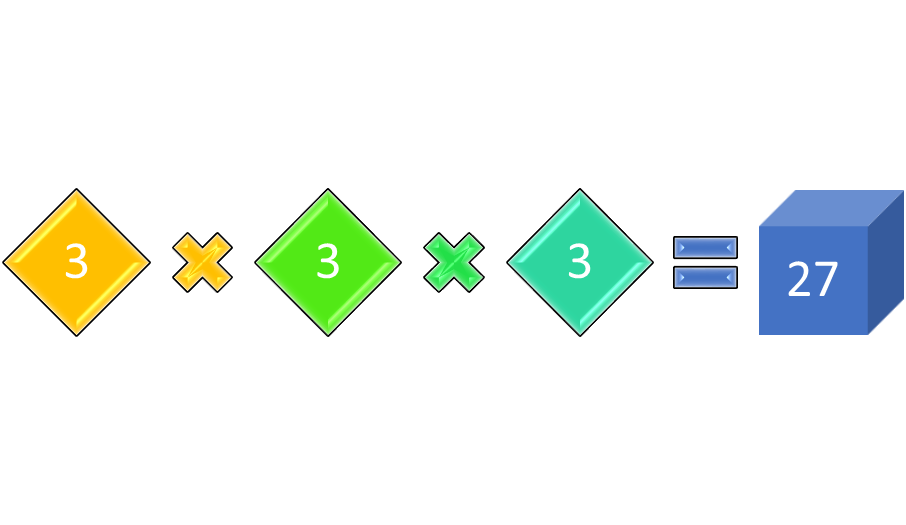Overview
Radical expressions are algebraic expressions that include roots, such as squares and cubes, variable expressions that include numerals, and expressions that can be factored as products of perfect squares or perfect cubes. Simplifying radical expressions is one way to more easily solve algebraic expressions that have them.
The Radical Symbol
The radical symbol √ gives the direction to take the root of the number or monomial that is under it. If there is no number in the index position of the radical √, the directions are to take the positive square root. If there is a number within the radical symbol (called the index), the directions are to take the level of root specified by the number. For example, a small number 3 in the index position stands for the cube root.
Figure 1: In order to solve a radical expression, use the index to determine the degree of root.
Perfect Squares and Perfect Cubes
A perfect square is a number or monomial that is the product of a number multiplied by itself. For example, 144 is a perfect square, because the number 122 (which is read as 12 squared) is equal to exactly 144. Similarly, 8 is a perfect cube, because the number 23 (which is read as 2 cubed) is equal to exactly 8. Radical expressions that contain real numbers that are perfect squares or perfect cubes are easily simplified.
Figure 2: Perfect squares and perfect cubes.
Imperfect Squares or Cubes
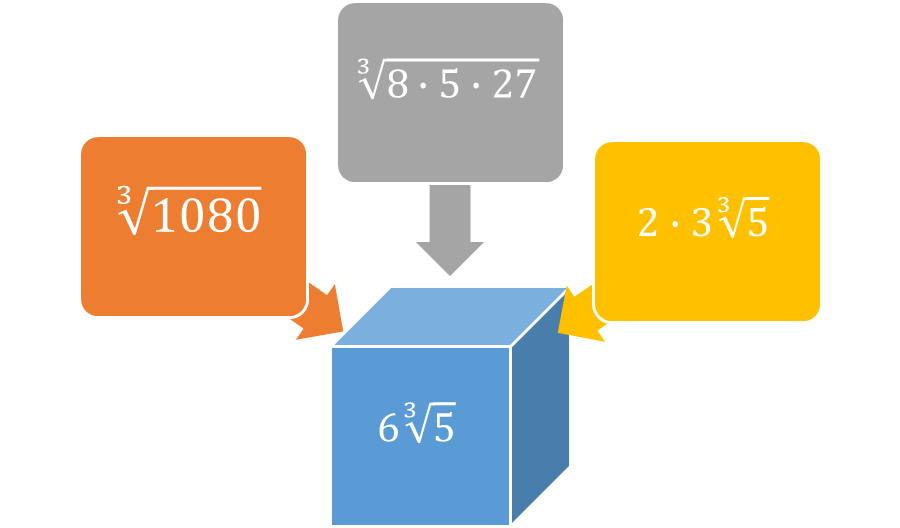
Many numbers can be simplified as factors of perfect squares or cubes and radicals that will have to be estimated. For example, √75 is the same thing as √3∙25 or 5√3. Suppose the expression were √75/10. It could be simplified as (5√3)/10 or √3/2. Similarly, the cube root of 135 is equal to the cube root of 27 times 5 or 3 times the cube root of 5.
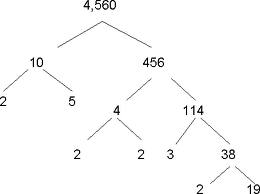
Figure 3: Simplifying the cube root of 1080.
Expressions That Contain Variables
Radical expressions that contain variables can be simplified similarly to radical expressions that contain real numbers. The expression √64r2 can be simplified to the square root of 64 or 8, times the square root of r2, or 8r. Both 64 and r2 are perfect squares. The expression √252r3 can be simplified to √36∙7∙r2∙r, or 6r√7r.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Edmonton, AB, Canada: visit Tutoring in Edmonton, AB, Canada