Overview
The trigonometric functions can also be defined in terms of the unit circle, so sometimes they are called the circular functions. This is because of the relationships of the trigonometric functions of angles to the unit circle. The trigonometric functions correspond to coordinates on the unit circle, also called terminal points.
Trigonometric Functions as Circular Functions
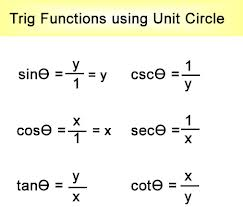
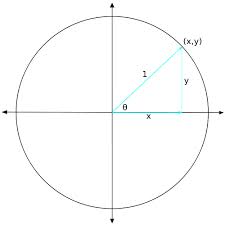
Locations along the unit circle are real numbers that can be expressed as x, y coordinates. Relationships between those numbers can be expressed as trigonometric functions. Suppose that t is a value on the unit circle, representing its distance from the (1, 0) coordinate. The terminal point (x, y) can be defined in math language so that the sine of t (sin t) equals y, the cosine of t (cos t) equals x, and the tangent of t (tan t) equals y/x, when x is not equal to 0. (Dividing by zero is undefined and is not allowed.)
More Trigonometric Functions as Circular Functions
The other trigonometric functions are also circular functions. The cosecant (csc) is the reciprocal of the sine, so that the cosecant of t equals 1/y, when y is not equal to 0. The secant (sec) is the reciprocal of the cosine, so that sec t is 1/x, when x is not equal to 0. The cotangent (cot) is the reciprocal of the tangent, so cot t equals x/y when y is not equal to 0.
Angles and the Unit Circle
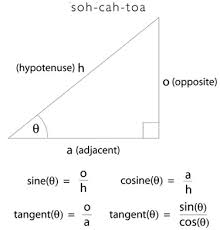
The trigonometric functions of angles and trigonometric functions measured in terms of the unit circle measure the same thing. Suppose that a right triangle is placed in the coordinate plane so that the vertex of the angle to be measured (call it theta θ) is on the center of the circle. The adjacent side to the right angle is along the x axis. In this example, the hypotenuse is 1, equal to the radius of the unit circle, but the sides of the triangle itself could extend beyond the unit circle.
Trigonometric Functions of the Angle
In terms of the right triangle, the trigonometric functions of the angle θ follow SOHCAHTOA. The sine of θ is opposite/hypotenuse, the cosine of θ is adjacent/hypotenuse, and the tangent of θ is opposite/adjacent. Note also that the arc between (0, 1) and (x, y) is equal to t, because it measures the same quantity.
Interested in pre-calculus tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Natchez, MS: visit: Tutoring in Natchez, MS