Overview
Solid objects have both volume and surface area. Formulas for calculations can be expressed using algebra, especially if the measurements of sides are stated by variables. The ratio of volume to surface area is important in applications in chemistry and biology.
Measurement of Volume
The volume of a solid is the amount of space that it contains. For example, the volume of a rectangular prism is measured as its length times width times height. In math language, V=lwh. The volume of a cylinder is π times the radius squared times the height of the cylinder, or V=πr2h. The volume of a cone is 1/3 πr2h, very similar to the formula of the volume of a cylinder. The volume of a pyramid is 1/3 lwh, which is similar to the formula for the volume of a rectangular prism, like a cube or a brick.
Measurement of Surface Area
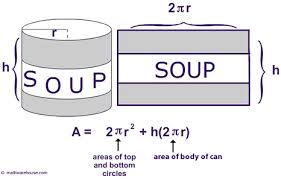
The surface area of a solid object is the total area contained in the two-dimensional surfaces of the solid object. (Think of the amount of wrap it would take to completely cover all surfaces without overlapping.) For example, the surface area of a rectangular prism is 2(lw +wh +lh). A cube has 6 faces, a top, bottom, and 4 sides. The surface area of a cylinder has 2 πr2+ 2πrh, because a cylinder has a top circle, a bottom circle, and the circular surface. The surface areas of cones and pyramids are more complex to calculate and depend on the orientation of the object.
Expressions Using Polynomials
Suppose the solid figure has measurements expressed in variables rather than constant numbers. For example, a rectangular prism has a length of c+1, a width of 2c, and a height of c-5. The volume of the rectangular prism would be (c +1)(2c)(c-5). The expression could be rearranged to (2c)[(c +1)(c-5)] using the Commutative and Associative Properties. The expression (c +1)(c-5) could be expanded to c2-4c -5. Multiply each part by 2c for 2c3-8c2 -10c.
Applications of Surface Area
The surface area of an object is important to various types of chemical reactions. For example, iron ground into a fine powder has a larger surface area than the same amount of iron in a block. It catches fire easily, while the block of iron is highly stable.
Interested in algebra tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Harrisburg, PA: visit: Tutoring in Harrisburg, PA