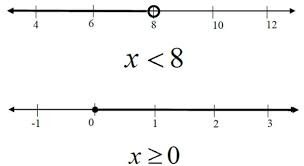Overview
If an inequality contains more than one operation, it will take more than one step to solve it. Suppose that in order to solve an inequality, both multiplication and addition statements need to be undone by using the multiplicative and additive inverses. As with other inequalities that take one step, the variable will have many correct solutions that can be graphed.
Undoing Multiple Steps
Study the Inequality
Study the inequality to see what operations it contains. Then, the inverses of those operations are used in order to solve it. Suppose the inequality is 260+ 4x≤ 500. It contains addition (260 + 4x) and multiplication (4x), so inverse operations of subtraction and division will be needed.
Solve Each Step
Before the variable can be isolated on one side of the inequality, the 260 must be moved away by subtracting its opposite, or inverse. 260 – 260 +4x ≤500 – 260, or 4x ≤ 240. Since x is still multiplied by 4, both sides of the inequality must be divided by 4, or 4x/4 ≤240/4 or x ≤60.
Reverse the Inequality Sign
Suppose the inequality is 6 -3y≤ 21. It contains subtraction (6-3y) and multiplication (3y), so the inverses addition and division must be used to solve it. Solving each step, 6-6-3y ≤21 -6 or -3y ≤21. Since y is multiplied by -3, both sides must be divided by -3. Dividing by a negative number adds an additional step, since the direction of the inequality sign must be reversed. Therefore -3y/-3 ≥21/-3, or y ≥-7.
Simplifying before Solving
Some inequalities must be simplified before they can be solved. Suppose (3 +9) > 7c -2. Using order of operations, the addition within parentheses must be solved first, and like terms are combined. The inequality 12> 7c -2 contains subtraction (7c-2) and multiplication (7c), so the inverses addition and division must be used. Isolating the variable, 12 +2 >7c -2 +2 or 14 >7c. Using the inverse, 14/7 >7c/7 or 2>c.
Distributive Property
Sometimes other properties must be used to simplify the inequality. Suppose the problem were 3 +2(x +4) ≥3. The distributive property can be used to expand 2(x +4) as 2x +8. Then 3 + 2x + 8 can be further combined as 11 +2x ≥3, or 2x ≥ 3- 11 , or 2x≥-8 or x ≥-4. Since both sides are divided by a positive number, the direction of the inequality sign is not reversed.
Graphing with a Number Line
Similar to the solutions of inequalities with one step, those with more than one step can be graphed on a number line. Remember the direction of the sign, so that the direction of the graph is correct. Also, if the sign is either < or >, the circle at the endpoint is open, while if the sign is ≤ or ≥, the circle at the endpoint is closed, showing the equals portion of the solution.
Interested in math tutoring services? Learn more about how we are assisting thousands of students each academic year.
SchoolTutoring Academy is the premier educational services company for K-12 and college students. We offer tutoring programs for students in K-12, AP classes, and college. To learn more about how we help parents and students in Fort Collins, CO: visit: Tutoring in Fort Collins, CO